Island Rotation Frequency
Equations (11.144) and (12.3) yield
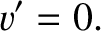 |
(12.4) |
It follows from Equation (11.136) that
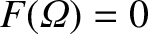 . Hence, Equations (11.113) and (11.130) imply that the
MHD stream-function of an isolated magnetic island chain takes the form
. Hence, Equations (11.113) and (11.130) imply that the
MHD stream-function of an isolated magnetic island chain takes the form
![\begin{displaymath}M({\mit\Omega})=-\frac{1}{1+\tau}\left(1-\alpha_\theta\,\frac...
...5ex]
1/\langle X^2\rangle&~~&{\mit\Omega}>1
\end{array}\right..\end{displaymath}](img3651.png) |
(12.5) |
Here,
 is a magnetic flux-surface label that takes the value zero at the
island O-points, unity on the magnetic separatrix, and is much larger that unity far from the island chain [see Equation (11.101)]. Moreover,
is a magnetic flux-surface label that takes the value zero at the
island O-points, unity on the magnetic separatrix, and is much larger that unity far from the island chain [see Equation (11.101)]. Moreover, 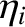 is a dimensionless measure of the ion temperature gradient at the rational surface [see Equation (4.4)], and
is a dimensionless measure of the ion temperature gradient at the rational surface [see Equation (4.4)], and 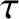 the ratio of the electron and ion pressure gradients at the rational surface
[see Equation (4.5)]. The quantity
the ratio of the electron and ion pressure gradients at the rational surface
[see Equation (4.5)]. The quantity
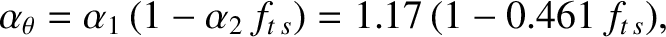 |
(12.6) |
where 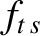 is the fraction of trapped particles at the rational surface [see Equation (2.202)], parameterizes the influence of ion neoclassical
poloidal flow-damping [see Equations (2.217), (2.218), and (11.5)].
Finally, the function
is the fraction of trapped particles at the rational surface [see Equation (2.202)], parameterizes the influence of ion neoclassical
poloidal flow-damping [see Equations (2.217), (2.218), and (11.5)].
Finally, the function
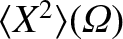 is specified in Section 8.11. Note that
is specified in Section 8.11. Note that
 as
as
 . It follows from Equation (12.5) that
. It follows from Equation (12.5) that
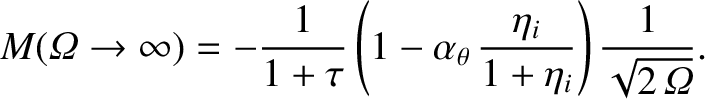 |
(12.7) |
However, Equations (11.109) and (12.4) yield
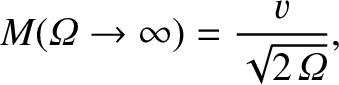 |
(12.8) |
where [see Equation (11.88)]
 |
(12.9) |
Here, 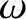 is the rotation
frequency of magnetic island chain in the laboratory frame (see Section 5.4),
is the rotation
frequency of magnetic island chain in the laboratory frame (see Section 5.4),
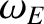 the E-cross-B frequency at the rational surface [see Equation (5.44)], and
the E-cross-B frequency at the rational surface [see Equation (5.44)], and
 the diamagnetic frequency at the rational surface [see Equation (5.47)].
The previous three equations give
the diamagnetic frequency at the rational surface [see Equation (5.47)].
The previous three equations give
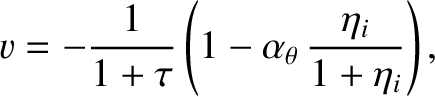 |
(12.10) |
which implies that
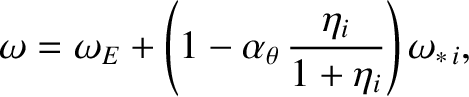 |
(12.11) |
where
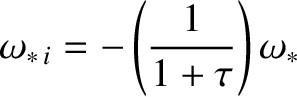 |
(12.12) |
is the ion diamagnetic frequency at the rational surface [see Equation (5.46)].
We conclude that, as a result of ion neoclassical poloidal flow-damping (i.e.,
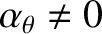 ), an isolated magnetic island chain does not exactly
co-rotate with the unperturbed ion fluid at the rational surface (i.e.,
), an isolated magnetic island chain does not exactly
co-rotate with the unperturbed ion fluid at the rational surface (i.e.,
 ). (Recall that non-neoclassical theory leads to the
prediction that a wide magnetic island chain does exactly co-rotate with the unperturbed ion fluid at the rational surface. See Section 9.5.)
Instead, assuming that
). (Recall that non-neoclassical theory leads to the
prediction that a wide magnetic island chain does exactly co-rotate with the unperturbed ion fluid at the rational surface. See Section 9.5.)
Instead, assuming that
 , and given that
, and given that
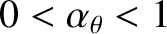 under most circumstances [see Equation (12.6)], we deduce that a wide magnetic island chain propagates in the electron diamagnetic direction with respect to the unperturbed ion fluid at the rational surface, but in
the ion diamagnetic direction with respect to the unperturbed MHD fluid [8,9,33]. This behavior should be contrasted with that of
a linear tearing mode, which propagates in the electron diamagnetic direction with respect to the unperturbed MHD fluid. (See Chapter 6.)
under most circumstances [see Equation (12.6)], we deduce that a wide magnetic island chain propagates in the electron diamagnetic direction with respect to the unperturbed ion fluid at the rational surface, but in
the ion diamagnetic direction with respect to the unperturbed MHD fluid [8,9,33]. This behavior should be contrasted with that of
a linear tearing mode, which propagates in the electron diamagnetic direction with respect to the unperturbed MHD fluid. (See Chapter 6.)
Figure: 12.1
Normalized perpendicular velocity profiles across the O-points (left-hand panel) and the X-points (right-hand panel)
of an isolated magnetic island chain in the island rest frame. The solid, dashed, and dotted
lines correspond to the electron, MHD, and ion fluids, respectively. Here, 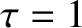 ,
, 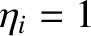 , and
, and
 . (See Table 11.1.)
. (See Table 11.1.)
|
|
According to Equations (8.75), (8.76), (11.130), and (12.5), the electron and ion fluid stream-functions take the respective forms
The poloidal components of the perpendicular velocities of the
electron, MHD, and ion fluids in the island rest frame are related to their respective stream-functions,  ,
,  , and
, and 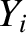 , according to Equations (8.72)–(8.74).
, according to Equations (8.72)–(8.74).
Figure 12.1 shows typical normalized perpendicular velocity profiles of the electron, MHD, and ion fluids across the O-points and
the X-points of an isolated magnetic island
chain in the island rest frame, as determined from Equations (8.72)–(8.74),
(12.5), (12.13), and (12.14). Here,  is the magnetic flux-surface minor radius,
is the magnetic flux-surface minor radius,
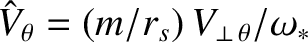 , and
, and  is the poloidal mode number of the tearing mode. It can be seen that all three fluids co-rotate with the island
chain inside the magnetic separatrix. However, unlike the non-neoclassical case (see Figure 9.3), ion neoclassical poloidal flow-damping (i.e.,
is the poloidal mode number of the tearing mode. It can be seen that all three fluids co-rotate with the island
chain inside the magnetic separatrix. However, unlike the non-neoclassical case (see Figure 9.3), ion neoclassical poloidal flow-damping (i.e.,
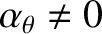 ) causes the ion fluid velocity profile
to be modified by the presence of the island chain.
In fact, all three velocity profiles
are discontinuous across the magnetic separatrix. As was explained in Section 8.9, these discontinuities are resolved in a thin layer of
thickness
) causes the ion fluid velocity profile
to be modified by the presence of the island chain.
In fact, all three velocity profiles
are discontinuous across the magnetic separatrix. As was explained in Section 8.9, these discontinuities are resolved in a thin layer of
thickness 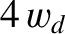 on the separatrix. It is clear from the figure that the island chain rotates in the ion diamagnetic (i.e., negative) direction with respect to
the unperturbed E-cross-B frame (i.e., the unperturbed MHD fluid) at the rational surface, but in the electron diamagnetic (i.e. positive) direction with respect to the unperturbed ion fluid.
on the separatrix. It is clear from the figure that the island chain rotates in the ion diamagnetic (i.e., negative) direction with respect to
the unperturbed E-cross-B frame (i.e., the unperturbed MHD fluid) at the rational surface, but in the electron diamagnetic (i.e. positive) direction with respect to the unperturbed ion fluid.
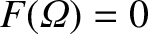 . Hence, Equations (11.113) and (11.130) imply that the
MHD stream-function of an isolated magnetic island chain takes the form
Here,
. Hence, Equations (11.113) and (11.130) imply that the
MHD stream-function of an isolated magnetic island chain takes the form
Here,
 is a magnetic flux-surface label that takes the value zero at the
island O-points, unity on the magnetic separatrix, and is much larger that unity far from the island chain [see Equation (11.101)]. Moreover,
is a magnetic flux-surface label that takes the value zero at the
island O-points, unity on the magnetic separatrix, and is much larger that unity far from the island chain [see Equation (11.101)]. Moreover, 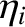 is a dimensionless measure of the ion temperature gradient at the rational surface [see Equation (4.4)], and
is a dimensionless measure of the ion temperature gradient at the rational surface [see Equation (4.4)], and 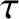 the ratio of the electron and ion pressure gradients at the rational surface
[see Equation (4.5)]. The quantity
where
the ratio of the electron and ion pressure gradients at the rational surface
[see Equation (4.5)]. The quantity
where 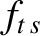 is the fraction of trapped particles at the rational surface [see Equation (2.202)], parameterizes the influence of ion neoclassical
poloidal flow-damping [see Equations (2.217), (2.218), and (11.5)].
Finally, the function
is the fraction of trapped particles at the rational surface [see Equation (2.202)], parameterizes the influence of ion neoclassical
poloidal flow-damping [see Equations (2.217), (2.218), and (11.5)].
Finally, the function
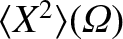 is specified in Section 8.11. Note that
is specified in Section 8.11. Note that
 as
as
 . It follows from Equation (12.5) that
. It follows from Equation (12.5) that
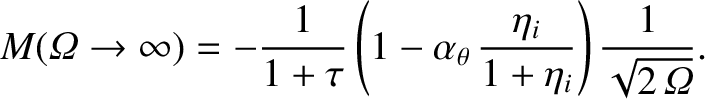
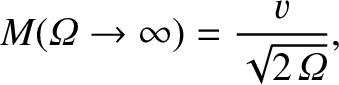

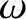 is the rotation
frequency of magnetic island chain in the laboratory frame (see Section 5.4),
is the rotation
frequency of magnetic island chain in the laboratory frame (see Section 5.4),
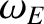 the E-cross-B frequency at the rational surface [see Equation (5.44)], and
the E-cross-B frequency at the rational surface [see Equation (5.44)], and
 the diamagnetic frequency at the rational surface [see Equation (5.47)].
The previous three equations give
the diamagnetic frequency at the rational surface [see Equation (5.47)].
The previous three equations give
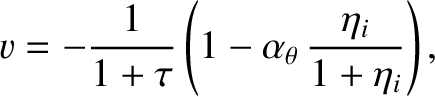
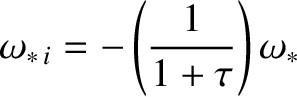
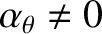 ), an isolated magnetic island chain does not exactly
co-rotate with the unperturbed ion fluid at the rational surface (i.e.,
), an isolated magnetic island chain does not exactly
co-rotate with the unperturbed ion fluid at the rational surface (i.e.,
 ). (Recall that non-neoclassical theory leads to the
prediction that a wide magnetic island chain does exactly co-rotate with the unperturbed ion fluid at the rational surface. See Section 9.5.)
Instead, assuming that
). (Recall that non-neoclassical theory leads to the
prediction that a wide magnetic island chain does exactly co-rotate with the unperturbed ion fluid at the rational surface. See Section 9.5.)
Instead, assuming that
 , and given that
, and given that
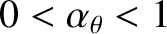 under most circumstances [see Equation (12.6)], we deduce that a wide magnetic island chain propagates in the electron diamagnetic direction with respect to the unperturbed ion fluid at the rational surface, but in
the ion diamagnetic direction with respect to the unperturbed MHD fluid [8,9,33]. This behavior should be contrasted with that of
a linear tearing mode, which propagates in the electron diamagnetic direction with respect to the unperturbed MHD fluid. (See Chapter 6.)
under most circumstances [see Equation (12.6)], we deduce that a wide magnetic island chain propagates in the electron diamagnetic direction with respect to the unperturbed ion fluid at the rational surface, but in
the ion diamagnetic direction with respect to the unperturbed MHD fluid [8,9,33]. This behavior should be contrasted with that of
a linear tearing mode, which propagates in the electron diamagnetic direction with respect to the unperturbed MHD fluid. (See Chapter 6.)
![\includegraphics[width=\textwidth]{Chapter12/Figure12_1.eps}](img3664.png)
 ,
,  , and
, and  , according to Equations (8.72)–(8.74).
, according to Equations (8.72)–(8.74).
 is the magnetic flux-surface minor radius,
is the magnetic flux-surface minor radius,
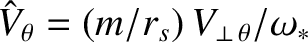 , and
, and  is the poloidal mode number of the tearing mode. It can be seen that all three fluids co-rotate with the island
chain inside the magnetic separatrix. However, unlike the non-neoclassical case (see Figure 9.3), ion neoclassical poloidal flow-damping (i.e.,
is the poloidal mode number of the tearing mode. It can be seen that all three fluids co-rotate with the island
chain inside the magnetic separatrix. However, unlike the non-neoclassical case (see Figure 9.3), ion neoclassical poloidal flow-damping (i.e.,
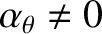 ) causes the ion fluid velocity profile
to be modified by the presence of the island chain.
In fact, all three velocity profiles
are discontinuous across the magnetic separatrix. As was explained in Section 8.9, these discontinuities are resolved in a thin layer of
thickness
) causes the ion fluid velocity profile
to be modified by the presence of the island chain.
In fact, all three velocity profiles
are discontinuous across the magnetic separatrix. As was explained in Section 8.9, these discontinuities are resolved in a thin layer of
thickness 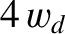 on the separatrix. It is clear from the figure that the island chain rotates in the ion diamagnetic (i.e., negative) direction with respect to
the unperturbed E-cross-B frame (i.e., the unperturbed MHD fluid) at the rational surface, but in the electron diamagnetic (i.e. positive) direction with respect to the unperturbed ion fluid.
on the separatrix. It is clear from the figure that the island chain rotates in the ion diamagnetic (i.e., negative) direction with respect to
the unperturbed E-cross-B frame (i.e., the unperturbed MHD fluid) at the rational surface, but in the electron diamagnetic (i.e. positive) direction with respect to the unperturbed ion fluid.