Next: Determination of Ion Flows Up: Plasma Fluid Theory Previous: Friction Force Densities Contents
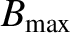 is the maximum value of
is the maximum value of 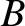 on the surface [34]. For a flux-surface with a circular poloidal
cross-section [38],
Thus, the average fraction of trapped particles on the flux-surface is
Note that the previous expression differs slightly from the less exact
expression (2.87).
on the surface [34]. For a flux-surface with a circular poloidal
cross-section [38],
Thus, the average fraction of trapped particles on the flux-surface is
Note that the previous expression differs slightly from the less exact
expression (2.87).
In the so-called banana collisionality regime,
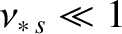 [see Equation (2.95)], the flux-surface averaged parallel viscous force densities take the form [22,34,43]
[see Equation (2.95)], the flux-surface averaged parallel viscous force densities take the form [22,34,43]
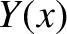 |
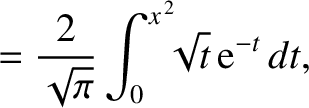 |
(2.207) |
 |
 |
(2.208) |
In the banana collisionality regime, the parallel viscous force arises from
collisional drag between passing and trapped particles [22,43]. The origin of this drag is the fact that, while passing particles can drift along
magnetic field-lines in one direction, trapped particles are forced to periodically reverse direction. Not surprisingly, the
viscous force density is proportional to the fraction of trapped particles, 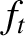 . [See Equation (2.203).]
. [See Equation (2.203).]