Next: Determination of Electron Flows Up: Plasma Fluid Theory Previous: Parallel Viscous Force Densities Contents
 smaller than the leading-order terms in the previous equation. This simplifying assumption
allows the ion parallel flow to be decoupled from the electron parallel flow [38].
It follows from Equations (2.183) and (2.212) that
smaller than the leading-order terms in the previous equation. This simplifying assumption
allows the ion parallel flow to be decoupled from the electron parallel flow [38].
It follows from Equations (2.183) and (2.212) that
![$\displaystyle ([F_{ii}] + f_t\,[\mu_i])\,(u_{\theta\,i}) = - [F_{ii}]\,(V_E) - [F_{ii}]\,(V_{\ast\,i}).$](img1019.png) |
(2.213) |
![$[F_{ii}]\,(V_E)= (0)$](img1020.png) because
because
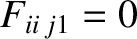 , for
, for 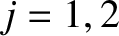 , and
, and
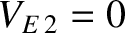 .
Thus, we get
where
.
Thus, we get
where
![$\displaystyle [L_{ii}]= ([F_{ii}+f_t\,[\mu_i])^{-1}\,[F_{ii}].$](img1023.png) |
(2.215) |
Employing Equation (2.193), and only retaining terms up to first order in the small parameter 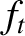 , we obtain
, we obtain
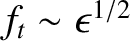 is
only a small parameter in the large aspect-ratio limit
is
only a small parameter in the large aspect-ratio limit
 .
.
It follows from Equations (2.165), (2.166), (2.170), (2.181)–(2.185), (2.214), and (2.216) that
and
Consider the circular magnetic flux-surface limit. In this limit,
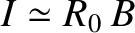 and
and
 ,
so
,
so
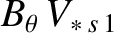 |
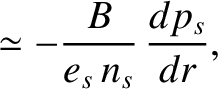 |
(2.223) |
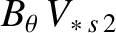 |
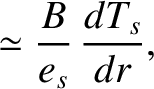 |
(2.224) |
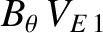 |
 |
(2.225) |
According to Equation (2.227), the poloidal component of the ion heat flux is equivalent to the poloidal component of the diamagnetic heat flux specified in
Equation (2.137), except that it is reduced by a factor
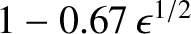 . The explanation for this reduction is that trapped
ions cannot carry a net poloidal heat flux around a magnetic flux-surface, because they are forced to periodically reverse their poloidal drift direction. Hence,
the diamagnetic ion heat flux is reduced by a factor that is roughly equal to the fraction of passing particles. [See Equation (2.201).]
This reduction is accomplished by the parallel heat flux specified in Equation (2.229).
. The explanation for this reduction is that trapped
ions cannot carry a net poloidal heat flux around a magnetic flux-surface, because they are forced to periodically reverse their poloidal drift direction. Hence,
the diamagnetic ion heat flux is reduced by a factor that is roughly equal to the fraction of passing particles. [See Equation (2.201).]
This reduction is accomplished by the parallel heat flux specified in Equation (2.229).
Equation (2.226) shows that the poloidal component of the ion fluid velocity is directly proportional to the poloidal component of the ion heat flux. The most surprising feature
of Equation (2.226) is the absence of a contribution from the E-cross-B velocity, despite the fact that this velocity possesses a non-zero poloidal component. [See Equation (2.138).] The explanation for this absence is that parallel friction forces drive an ion flow parallel to the magnetic
field that cancels out the poloidal component of the E-cross-B velocity, as well as the poloidal component of the ion diamagnetic velocity. The requisite flow, which is specified in Equation (2.228), is quite large, being a factor
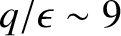 larger than a typical diamagnetic velocity. Equation (2.226) implies that a tokamak plasma is not free to rotate in the poloidal direction. In fact, any deviation of the ion poloidal flow velocity from the so-called neoclassical velocity specified by Equation (2.226) is
opposed by friction between trapped and passing ions, and consequently damps away on a timescale that is proportional to
larger than a typical diamagnetic velocity. Equation (2.226) implies that a tokamak plasma is not free to rotate in the poloidal direction. In fact, any deviation of the ion poloidal flow velocity from the so-called neoclassical velocity specified by Equation (2.226) is
opposed by friction between trapped and passing ions, and consequently damps away on a timescale that is proportional to  . This effect is
known as poloidal flow damping [48]. (See Section 2.24.)
. This effect is
known as poloidal flow damping [48]. (See Section 2.24.)
Incidentally, in the large aspect-ratio limit, Equation (2.189) reduces to
because the omitted term is![${\cal O}[(\epsilon/q)^2]$](img1057.png) smaller than the other terms. Thus, it follows from Equations (2.130), (2.165), (2.166), (2.181), and (2.186) that
smaller than the other terms. Thus, it follows from Equations (2.130), (2.165), (2.166), (2.181), and (2.186) that
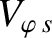 |
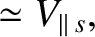 |
(2.231) |
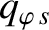 |
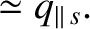 |
(2.232) |