Next: Useful Results Up: Plasma Fluid Theory Previous: Chew-Goldberger-Low Forms Contents
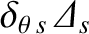 .
By analogy with the analysis Section 2.11, we can write [34]
for
.
By analogy with the analysis Section 2.11, we can write [34]
for 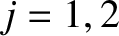 , where
, where
Taking the scalar product of Equations (2.163) and (2.164) with 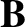 , and flux-surface averaging,
we annihilate the leading-order terms, to leave [34]
, and flux-surface averaging,
we annihilate the leading-order terms, to leave [34]
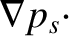

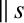 in Equation (2.164) depends on the
fact that
in Equation (2.164) depends on the
fact that

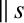 takes the Chew-Goldberger-Low form. [See Equation (2.154).]
takes the Chew-Goldberger-Low form. [See Equation (2.154).]
According to Equations (2.175) and (2.176), the parallel components of the friction force density and the electric force density drive both particle flows and heat flows along the magnetic field. These flows are opposed by the parallel viscous force density. We now need to solve the previous two equations to determine the parallel flows, which requires us to have expressions for the friction force density, as well as the parallel viscous force density.