Next: Toroidal Plasma Equilibrium Up: Plasma Fluid Theory Previous: Neoclassical Closure Scheme Contents
 toroidal magnetization parameter,
the species-
toroidal magnetization parameter,
the species- poloidal magnetization parameter,
poloidal magnetization parameter,
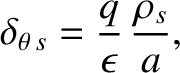 |
(2.111) |
 collisionality parameter,
collisionality parameter,
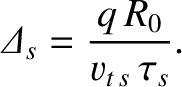 |
(2.112) |
In the following, we shall adopt the following fundamental ordering assumptions [32]:
Equation (2.113) is known as the drift ordering [18,29], and serves to rule out the rapid plasma motions associated with ideal magnetohydrodynamical instabilities [20]. Equation (2.114) is known as the transport ordering. According to this ordering, any time dependence of plasma quantities is due to the action of perpendicular transport, viscous heating, and frictional heating. The drift and transport orderings, combined with the analysis contained in the following two sections, imply that ,
,

 ,
,
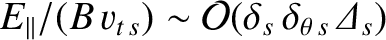 ,
,
 , and
, and
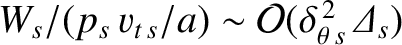 .
.
Equations (2.103)–(2.109) yield
where we have written [34]![$\displaystyle {\bf R}_s \simeq \frac{5}{2}\,\frac{T_s\,p_s}{m_s}\,{\bf I}+[\delta_{\theta\,s}\,{\mit\Delta}_s]\,{\bf r}_{\parallel\,s}.$](img820.png) |
(2.119) |
 or
or
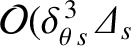 ) or
) or
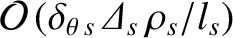 smaller than the leading-order terms, while retaining terms that are
smaller than the leading-order terms, while retaining terms that are
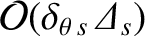 , which is only
self-consistent if
, which is only
self-consistent if
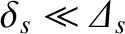 . As is shown in Table 2.4, the inequality
. As is shown in Table 2.4, the inequality
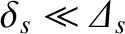 is well
satisfied for electrons in a tokamak fusion reactor, but is only barely satisfied for ions.
The
is well
satisfied for electrons in a tokamak fusion reactor, but is only barely satisfied for ions.
The
![$[\delta_{\theta\,s}\,{\mit\Delta}_s]$](img826.png) factors in the previous equations are there to
remind us that the terms they precede are
factors in the previous equations are there to
remind us that the terms they precede are
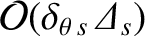 smaller than the leading-order terms.
Finally, it is helpful to define
smaller than the leading-order terms.
Finally, it is helpful to define