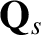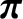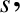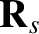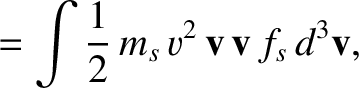Neoclassical Closure Scheme
As we have seen, plasmas that are confined in tokamak reactors are sufficiently collisionless that charged particles can travel around magnetic flux-surfaces very many times before the accumulated effect
of small-angle scattering events becomes significant. The classical collisional closure scheme described in Section 2.6 fails under such circumstances. The aim of Sections 2.8–2.21 is
to describe an alternative scheme, known as a neoclassical closure scheme, which is appropriate to
low-collisionality plasmas [52].
Now, the fluid equations for species- take the form:
take the form:
(See Section 2.3.)
However, the neoclassical closure scheme also requires the following third-order velocity-space moment of the kinetic equation [34]:
![$\displaystyle \frac{\partial {\bf Q}_s}{\partial t} = \frac{e_s}{m_s}\left[{\bf...
...f V}_s\right)+
{\bf Q}_s\times{\bf B}\right] -\nabla\cdot{\bf R}_s + {\bf G}_s,$](img793.png) |
(2.106) |
where
 take the form:
take the form:
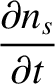
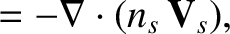
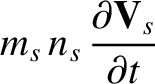

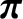
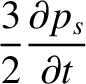
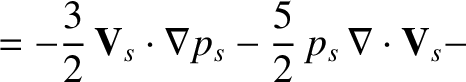
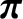

![$\displaystyle \frac{\partial {\bf Q}_s}{\partial t} = \frac{e_s}{m_s}\left[{\bf...
...f V}_s\right)+
{\bf Q}_s\times{\bf B}\right] -\nabla\cdot{\bf R}_s + {\bf G}_s,$](img793.png)