Fluid Theory
Plasma fluid equations are obtained by taking low-order velocity-space moments of the kinetic equation [18].
The low-order moments of the distribution function, 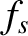 , all have simple physical interpretations.
First, we have the particle number density,
, all have simple physical interpretations.
First, we have the particle number density,
 |
(2.2) |
and the mean flow velocity,
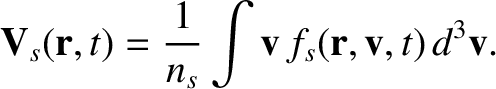 |
(2.3) |
Next, we have the pressure tensor,
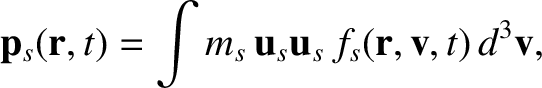 |
(2.4) |
and the heat flux,
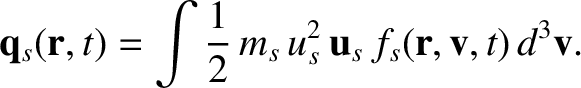 |
(2.5) |
Here,
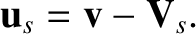 |
(2.6) |
The trace of the pressure tensor measures the ordinary (or scalar) pressure,
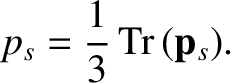 |
(2.7) |
The (kinetic) temperature is defined as
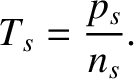 |
(2.8) |
The low-order velocity-space moments of the collision operator also have simple interpretations.
The friction force density takes the form
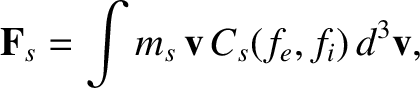 |
(2.9) |
whereas the collisional heating rate density (in the species- rest frame) is written
rest frame) is written
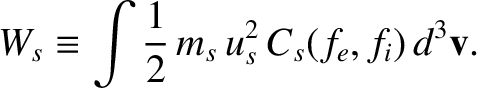 |
(2.10) |
The zeroth, first, and contracted second velocity-space moments of the kinetic equation, (2.1),
yield the following set of fluid equations for species- [18]:
[18]:
Here,
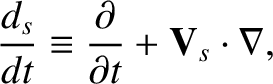 |
(2.14) |
is the well-known convective derivative, and
we have written
where 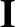 is the unit (identity) tensor, and
is the unit (identity) tensor, and

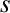 is the viscosity tensor. Obviously, Equation (2.11) is a particle conservation
equation for species-
is the viscosity tensor. Obviously, Equation (2.11) is a particle conservation
equation for species- , Equation (2.12) is a momentum conservation equation, and Equation (2.13) is an energy conservation equation [18].
, Equation (2.12) is a momentum conservation equation, and Equation (2.13) is an energy conservation equation [18].
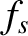 , all have simple physical interpretations.
First, we have the particle number density,
, all have simple physical interpretations.
First, we have the particle number density,

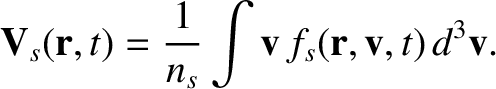
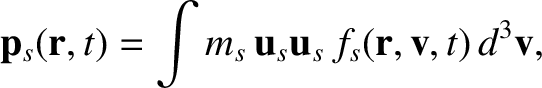
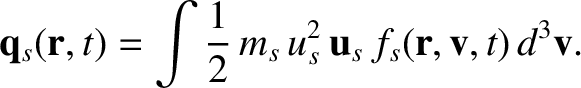
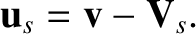
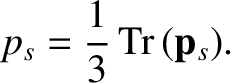
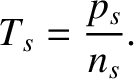
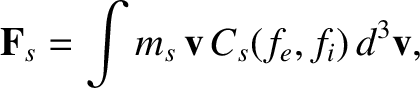
 rest frame) is written
rest frame) is written
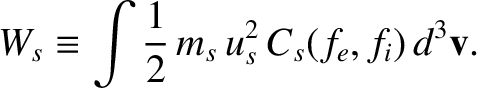
 [18]:
[18]:
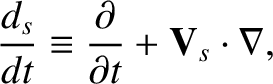
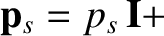
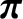
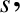
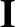 is the unit (identity) tensor, and
is the unit (identity) tensor, and

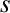 is the viscosity tensor. Obviously, Equation (2.11) is a particle conservation
equation for species-
is the viscosity tensor. Obviously, Equation (2.11) is a particle conservation
equation for species- , Equation (2.12) is a momentum conservation equation, and Equation (2.13) is an energy conservation equation [18].
, Equation (2.12) is a momentum conservation equation, and Equation (2.13) is an energy conservation equation [18].