Next: Fluid Closure Schemes Up: Plasma Fluid Theory Previous: Fluid Theory Contents
Of course, quasi-neutrality demands that [18]
We can estimate typical particle speeds in terms of the so-called thermal speed [18],
The typical gyro-radius of a charged particle gyrating in the magnetic field of a tokamak is given by
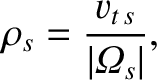 |
(2.18) |
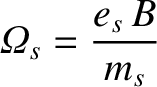 |
(2.19) |
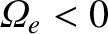 , indicating that electrons gyrate around magnetic field-lines in the opposite direction to ions.)
, indicating that electrons gyrate around magnetic field-lines in the opposite direction to ions.)
The electron-ion and ion-ion collision times are written
respectively [18]. Here,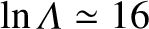 is
the Coulomb logarithm [42]. Note that
is
the Coulomb logarithm [42]. Note that 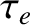 is the typical time required for the cumulative effect of electron-ion collisions to
deviate the path of an electron through
is the typical time required for the cumulative effect of electron-ion collisions to
deviate the path of an electron through 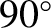 . Likewise,
. Likewise, 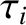 is the typical time required for the cumulative effect of ion-ion collisions to
deviate the path of an ion through
is the typical time required for the cumulative effect of ion-ion collisions to
deviate the path of an ion through 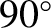 .
.
The electron and ion collision frequencies are simply the inverses of the corresponding 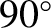 collision times:
collision times:
 |
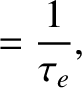 |
(2.22) |
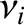 |
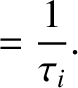 |
(2.23) |
Finally, the mean-free-paths between collisions (i.e., 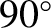 scattering events) for electrons and ions are
scattering events) for electrons and ions are
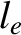 |
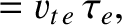 |
(2.24) |
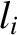 |
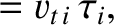 |
(2.25) |
Table 2.1 gives estimates for some of the fundamental plasma parameters defined in this section in a low-field and a high-field tokamak fusion reactor. Here, use has been made of
the data shown in Table 1.2. It has also been assumed that  , for the sake of simplicity.
, for the sake of simplicity.