Next: Particle Balance Up: Introduction Previous: Lawson Criterion Contents
 keV. Nevertheless, the two burning plasma experiments that are currently under construction, namely the ITER tokamak [55] and the SPARC tokamak [14], aim to operate at a somewhat lower volume-averaged plasma temperature of
keV. Nevertheless, the two burning plasma experiments that are currently under construction, namely the ITER tokamak [55] and the SPARC tokamak [14], aim to operate at a somewhat lower volume-averaged plasma temperature of
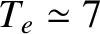 keV. Note that
keV. Note that
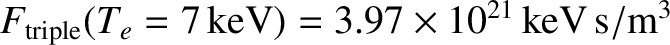 . Thus, confinement devices operating at this lower plasma temperature have to satisfy the slightly more stringent Lawson criterion
. Thus, confinement devices operating at this lower plasma temperature have to satisfy the slightly more stringent Lawson criterion
The total plasma pressure is written
Let be the strength of the magnetic field that confines the plasma. It is helpful to define the dimensionless parameter [21]
which measures the ratio of the plasma thermal energy density to the energy density of the magnetic field.
It turns out that plasma stability considerations ensure that conventional magnetic confinement devices, such as tokamaks, cannot
safely operate at beta values that exceed a few percent [59]. (See Section 1.10.)
be the strength of the magnetic field that confines the plasma. It is helpful to define the dimensionless parameter [21]
which measures the ratio of the plasma thermal energy density to the energy density of the magnetic field.
It turns out that plasma stability considerations ensure that conventional magnetic confinement devices, such as tokamaks, cannot
safely operate at beta values that exceed a few percent [59]. (See Section 1.10.)
We can write
where is the minor radius of the plasma (i.e., the shortest distance from the plasma core to the plasma
boundary), and
is the minor radius of the plasma (i.e., the shortest distance from the plasma core to the plasma
boundary), and
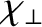 is the mean rate at which energy diffuses through the plasma. In practice,
energy diffuses out of a magnetic confinement device under the action of small-scale turbulence driven by density and temperature
gradients within the plasma [16,64]. Moreover, the typical energy diffusion rate is about
is the mean rate at which energy diffuses through the plasma. In practice,
energy diffuses out of a magnetic confinement device under the action of small-scale turbulence driven by density and temperature
gradients within the plasma [16,64]. Moreover, the typical energy diffusion rate is about
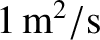 [64].
[64].
The previous four equations can be combined to give
Thus, we deduce that, in order to obtain a self-sustaining nuclear fusion reaction in a magnetic confinement device characterized by [see Equation (1.81)] and
[see Equation (1.81)] and
 , the product of the
magnetic field-strength and the plasma minor radius must exceed about 13 tesla-meters. Conventional superconducting magnet
technology limits practical magnetic field-strengths in magnetic confinement devices to approximately
, the product of the
magnetic field-strength and the plasma minor radius must exceed about 13 tesla-meters. Conventional superconducting magnet
technology limits practical magnetic field-strengths in magnetic confinement devices to approximately 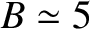 T. Thus, to achieve nuclear fusion,
such devices must have minor radii of about
T. Thus, to achieve nuclear fusion,
such devices must have minor radii of about
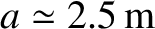 [55]. High-temperature superconducting magnet technology allows the
practically achievable magnetic field-strength to be increased to approximately
[55]. High-temperature superconducting magnet technology allows the
practically achievable magnetic field-strength to be increased to approximately
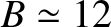 T. Thus, to achieve nuclear fusion,
high-field devices need only have minor radii of about
T. Thus, to achieve nuclear fusion,
high-field devices need only have minor radii of about
 , which implies a reduction in the plasma volume
by a factor of approximately 12 [14]. This is significant because the cost of a fusion experiment scales roughly as the volume of the experiment.
, which implies a reduction in the plasma volume
by a factor of approximately 12 [14]. This is significant because the cost of a fusion experiment scales roughly as the volume of the experiment.
The rules of thumb that
 and
and
 , combined with
Equations (1.23)–(1.25), allow us to make the estimates for the characteristic properties of a thermonuclear plasma trapped in both a low-field and
a high-field magnetic confinement device that are
given in Table 1.2. Note that these estimates accord well with the much more carefully worked out estimates given in References [55] and [14].
Roughly speaking, thermonuclear fusion requires a deuterium-tritium plasma with a minor radius of at least 1 meter, and an electron number density of at least
, combined with
Equations (1.23)–(1.25), allow us to make the estimates for the characteristic properties of a thermonuclear plasma trapped in both a low-field and
a high-field magnetic confinement device that are
given in Table 1.2. Note that these estimates accord well with the much more carefully worked out estimates given in References [55] and [14].
Roughly speaking, thermonuclear fusion requires a deuterium-tritium plasma with a minor radius of at least 1 meter, and an electron number density of at least 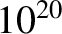 particles per cubic meter, to
be heated to a mean temperature of about 7 kilo-electronvolts, and the heat to be subsequently confined within the plasma for at least 1 second. The
requisite strength of the confining magnetic field is at least 5 telsa.
particles per cubic meter, to
be heated to a mean temperature of about 7 kilo-electronvolts, and the heat to be subsequently confined within the plasma for at least 1 second. The
requisite strength of the confining magnetic field is at least 5 telsa.
Of course, in order for magnetic confinement to work properly, the gyro-radii of all of the charged particle species must be significantly less than the
minor radius of the plasma. Obviously, the most stringent requirement is that the gyro-radii of alpha particle fusion products,
 , be less than the minor radius. Now,
, be less than the minor radius. Now,
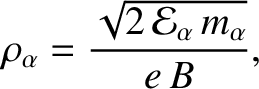 |
(1.26) |
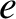 is the magnitude of the electron charge [21]. Table 1.2 gives
is the magnitude of the electron charge [21]. Table 1.2 gives
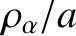 estimates for both low-field and high-field magnetic confinement
devices. In both cases,
estimates for both low-field and high-field magnetic confinement
devices. In both cases,
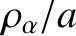 is significantly less than unity, indicating that the magnetic field is, in principle, strong enough to confine all of the
charged particles within the plasma. (See, in addition, Table 2.1.)
is significantly less than unity, indicating that the magnetic field is, in principle, strong enough to confine all of the
charged particles within the plasma. (See, in addition, Table 2.1.)