Next: Tearing Modes Up: Introduction Previous: Toroidal Pinches Contents
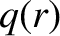 profile with a central value that is slightly less than unity [typically,
profile with a central value that is slightly less than unity [typically,
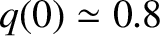 ] [64].
] [64].
Let
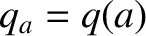 be the safety-factor at the edge of the plasma. One criterion that must be met if a tokamak plasma is to remain stable to ideal kink modes is [26]
be the safety-factor at the edge of the plasma. One criterion that must be met if a tokamak plasma is to remain stable to ideal kink modes is [26]
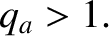 |
(1.77) |
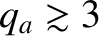 [64]. Now, a conventional tokamak has an inverse aspect-ratio of [14,55]
(See Table 1.2.)
It follows that
In other words, the strength of the toroidal magnetic field, which is needed to stabilize the plasma against ideal kink modes, exceeds that of the poloidal magnetic
field, which actually confines the plasma, by almost an order of magnitude. Obviously, this is a rather steep price to pay for plasma stability (given that most of the expense
of a tokamak experiment is associated with generating the toroidal magnetic field).
[64]. Now, a conventional tokamak has an inverse aspect-ratio of [14,55]
(See Table 1.2.)
It follows that
In other words, the strength of the toroidal magnetic field, which is needed to stabilize the plasma against ideal kink modes, exceeds that of the poloidal magnetic
field, which actually confines the plasma, by almost an order of magnitude. Obviously, this is a rather steep price to pay for plasma stability (given that most of the expense
of a tokamak experiment is associated with generating the toroidal magnetic field).
A second criterion that must be met if a tokamak plasma is to remain stable to ideal kink modes is [26]
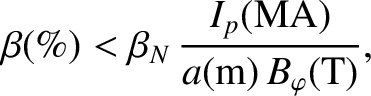 |
(1.80) |
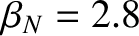 . This criterion is known as the Troyon limit [59], and sets an upper limit on the plasma pressure at fixed toroidal magnetic field-strength. [See Equation (1.23).]
The Troyon limit can also be expressed in the form
where use has been made of Equations (1.58) and (1.79). Thus, we can see that the maximum beta value at which a conventional tokamak
plasma can be safely operated is indeed limited to about 0.02. (See Section 1.5.)
. This criterion is known as the Troyon limit [59], and sets an upper limit on the plasma pressure at fixed toroidal magnetic field-strength. [See Equation (1.23).]
The Troyon limit can also be expressed in the form
where use has been made of Equations (1.58) and (1.79). Thus, we can see that the maximum beta value at which a conventional tokamak
plasma can be safely operated is indeed limited to about 0.02. (See Section 1.5.)