Next: Tokamaks Up: Introduction Previous: Linear Pinches Contents
An obvious way of dealing with the problem of the end plates is to bend a linear pinch into a circle to produce a toroidal plasma. See Figure 1.5. This procedure allows us to carry over most of the results that we previously obtained for a linear pinch while obviating the need for the end plates. In a so-called toroidal pinch, the plasma is confined on a series of axisymmetric, nested, toroidal magnetic flux-surfaces [26]. As such, the plasma thermal energy is not able to reach the toroidal vacuum vessel surrounding the plasma by freely streaming along magnetic field-lines, which, as we have seen, is a very rapid process, but must instead diffuse across the magnetic flux-surfaces, which is a comparatively slow process. The magnetic field of a toroidal pinch consists of a poloidal component that circulates about the magnetic axis, and a toroidal component that runs parallel to the axis. See Figure 1.5. The poloidal magnetic field is generated by a toroidal current that is induced in the plasma via transformer action. In essence, the plasma forms the single-turn secondary winding of a transformer circuit. The toroidal magnetic field is generated by currents flowing in magnetic field-coils that surround the plasma [64]. The poloidal magnetic field is responsible for confining the plasma via the pinch effect (when it is crossed with the toroidal plasma current). The toroidal magnetic field is needed to stabilize the plasma against ideal kink modes, but does not contribute greatly to confinement (other than by reducing the gyro-radii of charged particles within the plasma).
Let  and
and 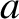 be the major and minor radii of the plasma torus, respectively. Consider an idealized magnetic flux-surface of circular poloidal cross-section.
Let
be the major and minor radii of the plasma torus, respectively. Consider an idealized magnetic flux-surface of circular poloidal cross-section.
Let 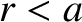 be the minor radius of this surface, and let
be the minor radius of this surface, and let  and
and  be poloidal and toroidal angles, respectively. Furthermore, let
be poloidal and toroidal angles, respectively. Furthermore, let
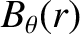 and
and 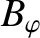 be the mean poloidal and toroidal magnetic field-strengths, respectively, on the surface. The safety-factor,
be the mean poloidal and toroidal magnetic field-strengths, respectively, on the surface. The safety-factor,
 ,
,  ,
,  coordinate system is right-handed, and that
coordinate system is right-handed, and that
 and
and
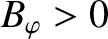 . This implies that
. This implies that
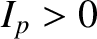 (in other words, the toroidal plasma current runs in the
(in other words, the toroidal plasma current runs in the 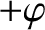 direction), and
direction), and 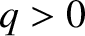 .
.