Next: Tearing Mode Rotation Up: Introduction Previous: Tokamaks Contents
 periods in the poloidal direction, and
periods in the poloidal direction, and 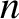 periods in the toroidal direction.
Here,
periods in the toroidal direction.
Here,  is termed the poloidal mode number, wheras
is termed the poloidal mode number, wheras 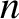 is termed the toroidal mode number.
Such a perturbation resonates with the plasma (i.e., satisfies
is termed the toroidal mode number.
Such a perturbation resonates with the plasma (i.e., satisfies
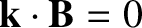 , where
, where 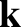 is the wavenumber of the perturbation, and
is the wavenumber of the perturbation, and
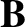 is the equilibrium magnetic field) at the magnetic flux-surface, of minor radius
is the equilibrium magnetic field) at the magnetic flux-surface, of minor radius 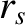 , at which [63]
, at which [63]
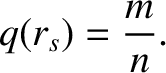 |
(1.82) |
An ideal kink mode is an instability of a tokamak plasma that is unstable even when the perturbed radial magnetic field is constrained to be zero at the associated rational surface (assuming that the surface lies within the plasma). As we have seen, such instabilities grow on the very short Alfvén time. Fortunately, ideal kink modes are relatively easy to avoid. In fact, ideal kink modes can be avoided by not allowing the edge safety-factor to fall significantly below 3, and not allowing the plasma beta to approach the Troyon limit. It is also necessary to prevent the plasma density from exceeding the so-called Greenwald limit [28] that is associated with the radiative collapse of the plasma current profile.
A tearing mode [27] is an instability of a tokamak plasma that is driven by the same free energy source as an ideal kink mode (namely, radial current and pressure gradients within the plasma [26]), but changes the topology of the magnetic field by tearing and reconnecting magnetic field-lines at the rational surface. This implies that the mode is not subject to the constraint that the perturbed radial magnetic field at the rational surface must be zero. Consequently, a tearing mode can be unstable even when the corresponding (i.e., possessing the same poloidal and toroidal mode numbers) ideal kink mode is stable [63].
Magnetic reconnection is made possible by finite plasma electrical resistivity [21]. Now, magnetic flux diffuses through a tokamak plasma, due to the action of resistivity, on the characteristic resistive time
where the plasma electrical conductivity is specified in Equation (1.61) [21]. As is shown in Table 1.5, the resistive time in a tokamak fusion reactor exceeds the Alfvén time by many orders of magnitude. To be more exact, the ratio of the two timescales, is known as the Lundquist number [21], and is of order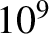 in a tokamak fusion reactor.
in a tokamak fusion reactor.
It is not surprising that a tearing mode grows and saturates on a timescale that is related to the resistive time [51]. In fact, the saturation time is
typically a few percent of the resistive time [29]. This implies that a tearing mode is an extremely slowly growing instability. Nevertheless,
the pulse duration of a tokamak plasma is generally sufficiently long for tearing instabilities to develop fully. As illustrated in Figure 1.6, a tearing mode changes the topology of the magnetic
field in the vicinity of the rational magnetic flux-surface to produce a magnetic island chain with  periods in the poloidal direction and
periods in the poloidal direction and 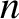 periods in the toroidal direction.
The chain typically has a radial width (defined as the width of the magnetic
separatrix that separates reconnected from unreconnected magnetic field-lines) that is a few percent of the plasma
minor radius. The presence of the island chain is significant because heat and particles are able to get from one (radial) side of the magnetic separatrix to the other by
rapidly streaming along magnetic field-lines, rather than having to slowly diffuse across magnetic flux-surfaces. Consequently, the plasma pressure
profile is flattened within the magnetic separatrix [19], giving rise to a degradation of the energy and particle confinement properties of the plasma [9].
Incidentally, the flattening of the electron temperature within the separatrix of a magnetic island allows the island structure to be imaged by an electron cyclotron emission
diagnostic [43,47].
periods in the toroidal direction.
The chain typically has a radial width (defined as the width of the magnetic
separatrix that separates reconnected from unreconnected magnetic field-lines) that is a few percent of the plasma
minor radius. The presence of the island chain is significant because heat and particles are able to get from one (radial) side of the magnetic separatrix to the other by
rapidly streaming along magnetic field-lines, rather than having to slowly diffuse across magnetic flux-surfaces. Consequently, the plasma pressure
profile is flattened within the magnetic separatrix [19], giving rise to a degradation of the energy and particle confinement properties of the plasma [9].
Incidentally, the flattening of the electron temperature within the separatrix of a magnetic island allows the island structure to be imaged by an electron cyclotron emission
diagnostic [43,47].