Tearing Mode Rotation
Under normal circumstances, a tearing mode in a tokamak plasma has a non-zero real frequency in the laboratory frame; this frequency is determined by the equilibrium plasma flow at the rational surface. In essence, a magnetic island chain is a helical pattern in the magnetic field generated by a helical current perturbation that is localized in the vicinity of the rational surface [51]. Given that plasma current is predominately carried by the electrons, it is natural to suppose that a magnetic island chain (as well as the tearing mode perturbation away from the rational surface) is convected by the electron fluid in the immediate vicinity of the rational surface. This is indeed the case in the so-called linear regime [1], in which the radial thickness of the island chain is less than the (very thin) characteristic linear layer width [27]. Of course, as a consequence of diamagnetic flows (see Section 2.11), if the island chain is convected by the electron fluid at the rational surface then it propagates with respect to the local ion fluid. However, this is not a problem because a linear layer is sufficiently thin that the magnetic field can diffuse through the plasma very rapidly, which implies that the ion fluid is not tied to the magnetic structure of the island chain. The situation is very different in the nonlinear regime, in which the radial thickness of the island chain exceeds the linear layer width. The region inside the magnetic separatrix of a nonlinear magnetic island chain is governed by a combination of flux-freezing and perturbed force balance [51]. This implies that both the electron and the ion fluids are trapped inside the separatrix, and are, therefore, forced to co-rotate with the island chain. There is no such constraint outside the separatrix, so the electron and ion fluids flow at different speeds in this region, as a consequence of diamagnetism. It follows that one or other of the electron and the ion fluid rotation profiles must exhibit a strong gradient across the separatrix. The island propagation velocity is determined by which of the two fluids is most resistant to the formation of such a gradient. Of course, it is the ion fluid which is more resistant because of its much greater viscosity [5,24,25]. (See Section 2.6.) Hence, a nonlinear magnetic island chain is convected by the ion fluid in the vicinity of the resonant surface, because this choice of propagation speed minimizes the ion fluid velocity gradient across the separatrix.
Interestingly, although early measurements of tearing mode rotation in tokamak plasmas suggested that tearing modes co-rotate with the electron
fluid at the rational surface [33,60], later measurements obtained the result that tearing modes co-rotate with the ion fluid [6,39]. The difference between
these two sets of results may be due to the fact that the early measurements were made in comparatively cold plasmas with comparatively wide linear layer widths (the layer width scales roughly as
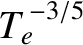 [21,27]).
[21,27]).
Rotating tearing modes in tokamaks are often observed to slow down, as they grow in amplitude, and finally stop rotating, or “lock”, with a definite poloidal and toroidal phase, when the mode exceeds a critical amplitude [11,56]. So-called locked modes are of concern because they are strongly correlated with sudden disruptions of the
plasma discharge [15]. The slowing down of the rotation of a growing tearing mode is associated with eddy currents excited in the resistive vacuum vessel surrounding the plasma; such currents generate a magnetic perturbation that exerts an electromagnetic torque at the rational surface that acts to brake the local plasma rotation, and, in turn,
brakes the rotation of the tearing mode [18,48]. (See Chapter 10.) The locking of the tearing mode is associated with a so-called error-field, which is an accidentally
produced, static, helical magnetic perturbation generated by misalignments of magnetic field-coils and uncompensated coil feeds. An error-field with the same
helicity as a tearing mode exerts an electromagnetic locking torque at the mode's rational surface that acts to arrest the rotation of the mode [18]. (See Chapter 13.)
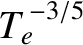 [21,27]).
[21,27]).