Next: Fusion Plasma Parameters Up: Introduction Previous: Nuclear Fusion Reactions Contents
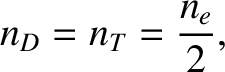 |
(1.10) |
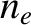 is the number density of electrons. Suppose that the two ions species have the same temperature,
is the number density of electrons. Suppose that the two ions species have the same temperature, 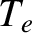 (measured in energy units), as the electrons. The total
thermal energy density of the plasma is thus [21]
The rate of nuclear fusion reactions per unit volume is [see Equation (1.6)]
(measured in energy units), as the electrons. The total
thermal energy density of the plasma is thus [21]
The rate of nuclear fusion reactions per unit volume is [see Equation (1.6)]
 |
(1.12) |
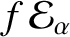 , must exceed the
energy loss rate per unit volume,
, must exceed the
energy loss rate per unit volume,
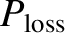 . (Recall that the alpha particles produced by nuclear fusion reactions heat the plasma, whereas the
neutrons exit the plasma without heating it.) Thus, we require
Let us write
Here, the energy confinement time,
. (Recall that the alpha particles produced by nuclear fusion reactions heat the plasma, whereas the
neutrons exit the plasma without heating it.) Thus, we require
Let us write
Here, the energy confinement time, 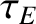 , is a measure of how long the plasma's thermal energy is confined within the plasma before escaping. Note that, at this stage, we are making no statement about the nature of the energy loss mechanism. In fact, Equation (1.14) can be thought of as the definition of
, is a measure of how long the plasma's thermal energy is confined within the plasma before escaping. Note that, at this stage, we are making no statement about the nature of the energy loss mechanism. In fact, Equation (1.14) can be thought of as the definition of 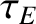 . The previous
four equations can be combined to give
where
. The previous
four equations can be combined to give
where
Figure 1.2 plots
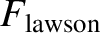 as a function of the electron temperature,
as a function of the electron temperature, 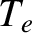 . It can be be seen that
. It can be be seen that
 attains a
minimum value of
attains a
minimum value of
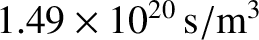 when
when
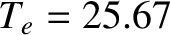 keV. Thus, we conclude that a self-sustaining nuclear fusion reaction is only possible in a
thermonuclear plasma if
keV. Thus, we conclude that a self-sustaining nuclear fusion reaction is only possible in a
thermonuclear plasma if
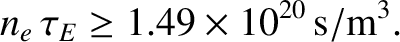 |
(1.17) |
In conventional magnetic confinement devices, 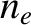 and
and 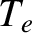 can be varied over a wide range of values. However, the maximum value of the plasma pressure, which is proportional to
can be varied over a wide range of values. However, the maximum value of the plasma pressure, which is proportional to  , is fixed by plasma stability considerations [26,64]. (See Section 1.10.) Now, according to Equations (1.15) and (1.16), the
criterion for a self-sustaining nuclear fusion reaction can be recast in the form
, is fixed by plasma stability considerations [26,64]. (See Section 1.10.) Now, according to Equations (1.15) and (1.16), the
criterion for a self-sustaining nuclear fusion reaction can be recast in the form
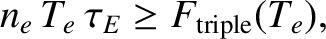 |
(1.18) |
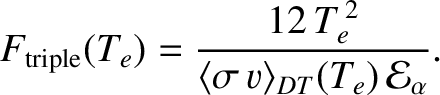 |
(1.19) |
 is fixed, it follows that fusion reactivity is maximized at the temperature that
minimizes the function
is fixed, it follows that fusion reactivity is maximized at the temperature that
minimizes the function
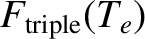 . As illustrated in Figure 1.3,
. As illustrated in Figure 1.3,
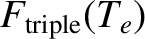 attains a
minimum value of
attains a
minimum value of
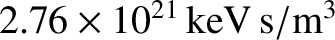 when
when
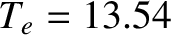 keV. Thus, a more useful form of the Lawson criterion is
keV. Thus, a more useful form of the Lawson criterion is
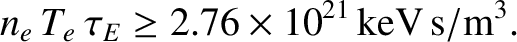 |
(1.20) |
 is known as the fusion triple product, and is the conventional figure of merit for thermonuclear fusion reactions in magnetic confinement devices [64].
is known as the fusion triple product, and is the conventional figure of merit for thermonuclear fusion reactions in magnetic confinement devices [64].