Next: Lawson Criterion Up: Introduction Previous: Thermonuclear Fusion Contents
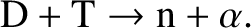 |
(1.1) |
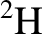 ), T denotes a tritium nucleus (
), T denotes a tritium nucleus (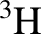 ), n denotes a neutron, and
), n denotes a neutron, and
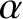 denotes an alpha particle (
denotes an alpha particle (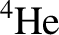 ). At achievable mean plasma temperatures (i.e., less than about 10 keV), a D-T fusion reaction has a cross-section that
is approximately 100 times greater than that of a D-D fusion reaction (or a T-T fusion reaction) [2]. (There is, unfortunately, no H-H fusion reaction.) For this reason, D-T fusion is considered to be
more practical than D-D fusion, despite the fact that there is no natural source of tritium on the Earth. In fact, it is envisaged that D-T
fusion reactors will breed the requisite tritium within a blanket that surrounds the plasma via nuclear reactions such as
). At achievable mean plasma temperatures (i.e., less than about 10 keV), a D-T fusion reaction has a cross-section that
is approximately 100 times greater than that of a D-D fusion reaction (or a T-T fusion reaction) [2]. (There is, unfortunately, no H-H fusion reaction.) For this reason, D-T fusion is considered to be
more practical than D-D fusion, despite the fact that there is no natural source of tritium on the Earth. In fact, it is envisaged that D-T
fusion reactors will breed the requisite tritium within a blanket that surrounds the plasma via nuclear reactions such as
 |
(1.2) |
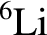 makes up 7.6% of terrestrial lithium, which makes up about 0.002% of the Earth's crust.
makes up 7.6% of terrestrial lithium, which makes up about 0.002% of the Earth's crust.
A D-T fusion reaction liberates
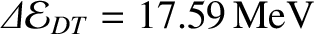 |
(1.3) |
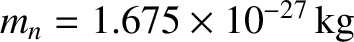 and
and
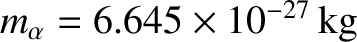 , respectively. Hence, the
kinetic energies of the neutron and the alpha particle generated by a D-T fusion reaction are
, respectively. Hence, the
kinetic energies of the neutron and the alpha particle generated by a D-T fusion reaction are
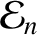 |
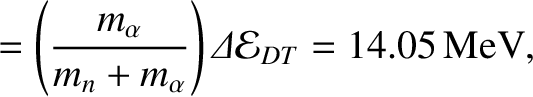 |
(1.4) |
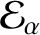 |
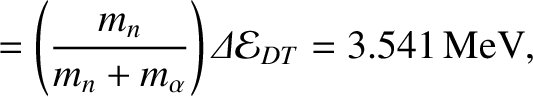 |
(1.5) |
![\includegraphics[width=1.\textwidth]{Chapter01/Figure1_1.eps}](img167.png)
|
Consider a thermonuclear plasma consisting, principally, of electrons, deuterium ions (that are fully stripped of electrons), and (fully-stripped) tritium ions. All three species are assumed to have have Maxwellian
velocity distribution functions characterized by a common temperature, 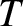 . The rate of D-T fusion reactions occurring per unit volume within the plasma is [50]
. The rate of D-T fusion reactions occurring per unit volume within the plasma is [50]
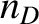 is the deuteron number density,
is the deuteron number density, 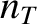 the triton number density,
the triton number density, 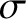 the cross-section for D-T fusion reactions,
the cross-section for D-T fusion reactions, 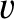 the relative
velocity of the reacting species, and
the relative
velocity of the reacting species, and
 denotes an average over the Maxwellian distributions of the reacting species. In the range of temperatures
denotes an average over the Maxwellian distributions of the reacting species. In the range of temperatures
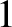 –
–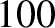 keV, the D-T fusion reactivity,
keV, the D-T fusion reactivity,
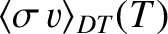 , is accurately fitted by the following formula [2,4]
where
Here,
, is accurately fitted by the following formula [2,4]
where
Here, 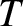 is measured in units of keV. The parameters
is measured in units of keV. The parameters  –
–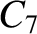 are specified in Table 1.1.
Figure 1.1 plots
are specified in Table 1.1.
Figure 1.1 plots
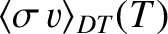 for a realistic range of plasma temperatures. It can be seen that
for a realistic range of plasma temperatures. It can be seen that
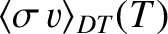 is a rapidly increasing function of increasing temperature, and that
is a rapidly increasing function of increasing temperature, and that
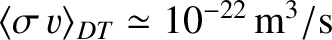 when
when
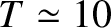 keV.
keV.