Next: Nuclear Fusion Reactions Up: Introduction Previous: Introduction Contents
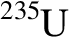 and
and
 ). On the other hand, a nuclear
fusion reactor would derive energy from the fusion of light nuclei (i.e.,
). On the other hand, a nuclear
fusion reactor would derive energy from the fusion of light nuclei (i.e., 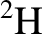 and
and 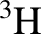 ). The main advantages of
nuclear fusion reactors are, firstly, that they do not generate heat-producing, highly-radioactive, long-lived fission products, and, secondly, that the
principal fuel for such reactors (namely, deuterium) is abundantly present on the Earth. In fact, deuterium has a natural abundance in the Earth's oceans of about one atom in 6420 of hydrogen.
). The main advantages of
nuclear fusion reactors are, firstly, that they do not generate heat-producing, highly-radioactive, long-lived fission products, and, secondly, that the
principal fuel for such reactors (namely, deuterium) is abundantly present on the Earth. In fact, deuterium has a natural abundance in the Earth's oceans of about one atom in 6420 of hydrogen.
In order for two light nuclei to fuse together they must collide with sufficient violence that one of the nuclei is able to quantum mechanically tunnel through the other's repulsive Coulomb barrier [2]. In so-called thermonuclear fusion, both species of nuclei are confined within a plasma, and have thermal (i.e., Maxwellian) velocity distribution functions characterized by a common temperature. The collisions that give rise to nuclear fusion reactions are associated with the random motions of the nuclei within the plasma, and have mean energies (in the center of mass frame) that are directly proportional to the plasma temperature. Thus, the higher the temperature, the more violent the collisions. It follows that if the temperature is made sufficiently high then nuclear fusion will occur. However, a high-temperature plasma is, necessarily, also a high-pressure plasma, and, thus, requires confinement to prevent it from dispersing. The thermonuclear plasma at the center of the Sun is confined by gravity. Unfortunately, gravity is too weak a force to confine a terrestrial thermonuclear plasma of realistic size. Instead, such plasmas can be confined by a strong magnetic field. In principle, magnetic confinement is possible if the gyro-radii of the charged particles that make up the plasma are much smaller than the plasma dimensions [21].