Next: Energy Balance Up: Introduction Previous: Fusion Plasma Parameters Contents
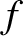 is the rate of nuclear fusion reactions per unit volume. [See Equation (1.6).] Moreover,
is the rate of nuclear fusion reactions per unit volume. [See Equation (1.6).] Moreover, 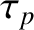 is the
particle confinement time, which is defined as the average time that a particle is confined within the plasma. The deuterons,
tritons, and helium ash particles are assumed to have the same particle confinement times, for the sake of simplicity. Finally,
is the
particle confinement time, which is defined as the average time that a particle is confined within the plasma. The deuterons,
tritons, and helium ash particles are assumed to have the same particle confinement times, for the sake of simplicity. Finally, 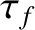 is the
fueling time, which is the average time on which fusion reagents are replenished in the plasma (e.g., via the injection of
frozen deuterium/tritium pellets) [12]. We are
assuming that deuterons and tritons are replenished at the same rate. Of course, there is no helium ash particle fueling (other than that provided by
nuclear fusion reactions).
is the
fueling time, which is the average time on which fusion reagents are replenished in the plasma (e.g., via the injection of
frozen deuterium/tritium pellets) [12]. We are
assuming that deuterons and tritons are replenished at the same rate. Of course, there is no helium ash particle fueling (other than that provided by
nuclear fusion reactions).
Suppose that the plasma has attained a steady state (i.e.,  ). Let us assumed that
). Let us assumed that 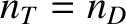 (i.e., the deuterium-tritium mix
is optimal for nuclear fusion). The burn fraction,
(i.e., the deuterium-tritium mix
is optimal for nuclear fusion). The burn fraction,
 |
(1.30) |
Quasi-neutrality [21] demands that
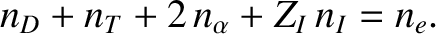 |
(1.33) |
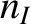 and
mean charge number
and
mean charge number 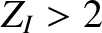 . Usually, such ions originate from the interaction between the plasma and the
surrounding solid surfaces. Typical impurity ion species are beryllium, boron, carbon, or tungsten. The effective charge number of
the plasma ions is defined [64]
The pervious six equations can be combined with
Equation (1.6) to give
Here, we have written
where
. Usually, such ions originate from the interaction between the plasma and the
surrounding solid surfaces. Typical impurity ion species are beryllium, boron, carbon, or tungsten. The effective charge number of
the plasma ions is defined [64]
The pervious six equations can be combined with
Equation (1.6) to give
Here, we have written
where  is the mean rate at which particles diffuse through the plasma. In practice,
particles diffuse out of a magnetic confinement device under the action of small-scale turbulence driven by density and temperature
gradients within the plasma [16,64]. Moreover, the typical particle diffusion rate is about
is the mean rate at which particles diffuse through the plasma. In practice,
particles diffuse out of a magnetic confinement device under the action of small-scale turbulence driven by density and temperature
gradients within the plasma [16,64]. Moreover, the typical particle diffusion rate is about
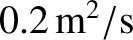 [64].
[64].
Assuming that
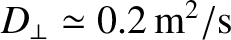 ,
,
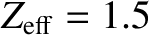 [14,55], and
[14,55], and 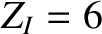 (which corresponds to fully-stripped carbon impurity ions), making use of the
data given in Table 1.2, and employing Equations (1.31) and (1.34)–(1.38), we can derive the particle balance data given in Table 1.3. [Incidentally, Equation (1.37) is most easily solved for
(which corresponds to fully-stripped carbon impurity ions), making use of the
data given in Table 1.2, and employing Equations (1.31) and (1.34)–(1.38), we can derive the particle balance data given in Table 1.3. [Incidentally, Equation (1.37) is most easily solved for 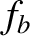 via iteration.]
Note that, for both low-field and high-field confinement devices, the
burn fraction is only about 5%. In other words, only 5% of the fuel ions injected into the plasma undergo nuclear fusion reactions; the remainder escape. Unfortunately, this is
necessary, otherwise there would be an unacceptable build up of helium ash within the plasma. [See Equation (1.32).] In fact, we estimate the helium ash to
make up about 3% percent of the ion content of the plasma. The presence of helium ash and impurity ions in the plasma dilutes the concentration of
fuel ions, with respect to that which would be present if the helium ash and impurities were absent, by about 14%. This, in turn, reduces the nuclear fusion reaction rate in the plasma
by about 25%. We conclude that the helium ash and impurity ion contents of the plasma must be kept as low as possible. Incidentally heavy impurity ions, such as tungsten,
have such a high mean charge number in a thermonuclear plasma (about 60, in the case of tungsten) that their relative concentration must be significantly less than
that given in Table 1.3 (about
via iteration.]
Note that, for both low-field and high-field confinement devices, the
burn fraction is only about 5%. In other words, only 5% of the fuel ions injected into the plasma undergo nuclear fusion reactions; the remainder escape. Unfortunately, this is
necessary, otherwise there would be an unacceptable build up of helium ash within the plasma. [See Equation (1.32).] In fact, we estimate the helium ash to
make up about 3% percent of the ion content of the plasma. The presence of helium ash and impurity ions in the plasma dilutes the concentration of
fuel ions, with respect to that which would be present if the helium ash and impurities were absent, by about 14%. This, in turn, reduces the nuclear fusion reaction rate in the plasma
by about 25%. We conclude that the helium ash and impurity ion contents of the plasma must be kept as low as possible. Incidentally heavy impurity ions, such as tungsten,
have such a high mean charge number in a thermonuclear plasma (about 60, in the case of tungsten) that their relative concentration must be significantly less than
that given in Table 1.3 (about
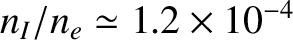 , in the case of tungsten) in order to avoid unacceptable fuel ion dilution.
, in the case of tungsten) in order to avoid unacceptable fuel ion dilution.
If thermonuclear fusion is to work properly then the time required for alpha particle fusion products to slow down due to collisions with thermal particles, and, thereby, heat the plasma, must be much less than the particle confinement time. (Here, we are making the simplifying assumption that thermonuclear alpha particles have the same confinement time as the thermalized plasma species.) Otherwise, alpha particles would be able to escape from the plasma without giving up all of their fusion energy. The slowing-down time for alpha particles is given approximately by [21,57,58]
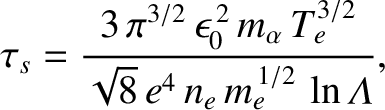 |
(1.39) |
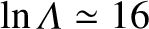 is the Coulomb logarithm [21], and
is the Coulomb logarithm [21], and 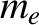 the electron mass. As shown in Table 1.3, the ratio
the electron mass. As shown in Table 1.3, the ratio
 is indeed very much less than unity in
thermonuclear magnetic confinement devices.
is indeed very much less than unity in
thermonuclear magnetic confinement devices.