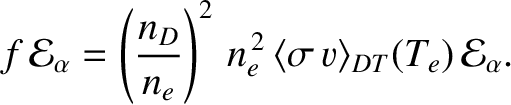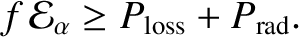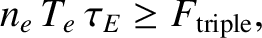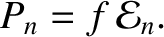Let now perform the energy balance calculation outlined in Section 1.4 more exactly. In the
presence of helium ash and impurities, the expression, (1.11), for the total thermal energy density of the plasma generalizes to give
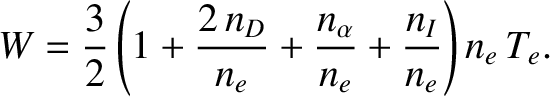 |
(1.40) |
As before, the energy loss rate per unit volume due to the turbulent transport of thermal energy out of the plasma is given by [see Equation (1.14)]
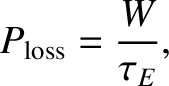 |
(1.41) |
where 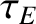 is the energy confinement time. However, fusion plasmas also lose energy due to the emission of electromagnetic radiation (because they are optically thin).
In fact, the principal radiation loss mechanism is electron-ion bremsstrahlung. The energy loss rate per unit volume
due to electron-ion bremsstrahlung is
is the energy confinement time. However, fusion plasmas also lose energy due to the emission of electromagnetic radiation (because they are optically thin).
In fact, the principal radiation loss mechanism is electron-ion bremsstrahlung. The energy loss rate per unit volume
due to electron-ion bremsstrahlung is
 |
(1.42) |
where
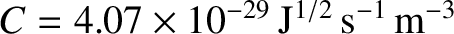 [50]. Impurity ions that are not fully stripped of electrons can also radiate via line emission [35]. For light impurities, such as carbon, which are fully stripped in the plasma core, such radiation is
concentrated at the edge of the plasma, and is relatively unimportant. On the other hand, heavy impurities, such as tungsten, are not fully stripped in the plasma core, and therefore emit line radiation
throughout the plasma. The energy loss due to line radiation from heavy impurities is typically similar in magnitude to the energy loss due to bremsstrahlung [14,35].
As before, the heating power per unit volume due to
nuclear fusion reactions is
[50]. Impurity ions that are not fully stripped of electrons can also radiate via line emission [35]. For light impurities, such as carbon, which are fully stripped in the plasma core, such radiation is
concentrated at the edge of the plasma, and is relatively unimportant. On the other hand, heavy impurities, such as tungsten, are not fully stripped in the plasma core, and therefore emit line radiation
throughout the plasma. The energy loss due to line radiation from heavy impurities is typically similar in magnitude to the energy loss due to bremsstrahlung [14,35].
As before, the heating power per unit volume due to
nuclear fusion reactions is
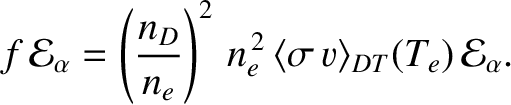 |
(1.43) |
[See Equation (1.6).]
The criterion that must be satisfied to obtain a self-sustaining nuclear fusion reaction is
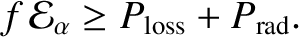 |
(1.44) |
[See Equation (1.13).]
The previous equations can be rearranged to give
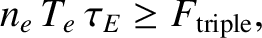 |
(1.45) |
where
![$\displaystyle F_{\rm triple} = \left(\frac{n_e}{n_D}\right)^2\frac{\left[\frac{...
..._e^{\,3/2}\,\tau_E\right]}
{\langle\sigma v\rangle_{DT}(T_e)\,{\cal E}_\alpha}.$](img303.png) |
(1.46) |
Finally, the energy per unit time per unit plasma volume that ends up being absorbed in the blanket via neutron emission is
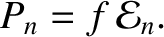 |
(1.47) |
Hence, the fractions of the nuclear fusion energy generated within the plasma that end up being absorbed in the blanket, being lost as heat conducted to the plasma facing components, and being radiated away, are
respectively.
Table: 1.4
More characteristic properties of a thermonuclear plasma trapped in a low-field and a high-field magnetic confinement device. Here,
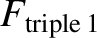 is the critical fusion triple product needed for self-sustained nuclear fusion in the absence of both ion dilution and
radiation losses,
is the critical fusion triple product needed for self-sustained nuclear fusion in the absence of both ion dilution and
radiation losses,
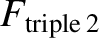 the critical fusion triple product in the presence of ion dilution and
the absence of radiation losses,
the critical fusion triple product in the presence of ion dilution and
the absence of radiation losses,
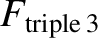 the critical fusion triple product in the presence of both ion dilution and
radiation losses,
the critical fusion triple product in the presence of both ion dilution and
radiation losses, 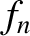 the fraction of the nuclear fusion energy generated within the plasma that is absorbed by the blanket,
the fraction of the nuclear fusion energy generated within the plasma that is absorbed by the blanket,
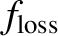 the fraction of
the fusion energy that is lost as heat conducted to the plasma facing components, and
the fraction of
the fusion energy that is lost as heat conducted to the plasma facing components, and
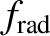 the fraction of the fusion energy that is radiated away.
the fraction of the fusion energy that is radiated away.
| |
Low-Field |
High-Field |
 |
5.0 |
12.0 |
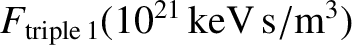 |
3.97 |
3.97 |
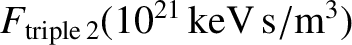 |
5.04 |
5.09 |
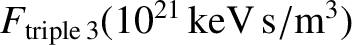 |
6.84 |
7.09 |
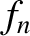 |
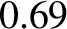 |
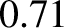 |
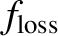 |
 |
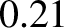 |
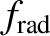 |
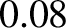 |
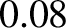 |
|
The information in Tables 1.2 and 1.3 can be used, in combination with Equations (1.46) and (1.48)–(1.50), to produce the estimates that are given in Table 1.4. It can be seen that the
dilution of the fusion reagent ions due to the presence of helium ash and impurities increases the critical fusion triple product needed for self-sustained nuclear fusion by about 30%. Radiation
losses increase the critical fusion triple product by, at least (because we have neglected impurity line radiation), a further 40%. Thus, the table highlights the importance of keeping the helium ash and impurity
content of the plasma as small as possible. Note, however, that, even in a pure D-T plasma, there is an irreducible radiation loss due to bremsstrahlung between the electrions and the fueling ions that
increases the critical triple product over that specified in Equation (1.21) by about 25%. Finally, about 70% of the fusion energy created within the plasma is absorbed by
the blanket, about 22% is lost as heat conducted to the plasma facing components, and about 8% is radiated away.
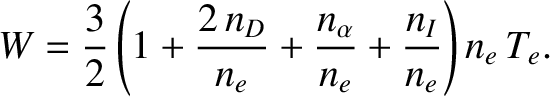
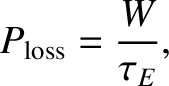
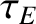 is the energy confinement time. However, fusion plasmas also lose energy due to the emission of electromagnetic radiation (because they are optically thin).
In fact, the principal radiation loss mechanism is electron-ion bremsstrahlung. The energy loss rate per unit volume
due to electron-ion bremsstrahlung is
is the energy confinement time. However, fusion plasmas also lose energy due to the emission of electromagnetic radiation (because they are optically thin).
In fact, the principal radiation loss mechanism is electron-ion bremsstrahlung. The energy loss rate per unit volume
due to electron-ion bremsstrahlung is

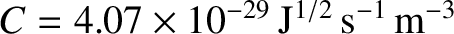 [50]. Impurity ions that are not fully stripped of electrons can also radiate via line emission [35]. For light impurities, such as carbon, which are fully stripped in the plasma core, such radiation is
concentrated at the edge of the plasma, and is relatively unimportant. On the other hand, heavy impurities, such as tungsten, are not fully stripped in the plasma core, and therefore emit line radiation
throughout the plasma. The energy loss due to line radiation from heavy impurities is typically similar in magnitude to the energy loss due to bremsstrahlung [14,35].
As before, the heating power per unit volume due to
nuclear fusion reactions is
[50]. Impurity ions that are not fully stripped of electrons can also radiate via line emission [35]. For light impurities, such as carbon, which are fully stripped in the plasma core, such radiation is
concentrated at the edge of the plasma, and is relatively unimportant. On the other hand, heavy impurities, such as tungsten, are not fully stripped in the plasma core, and therefore emit line radiation
throughout the plasma. The energy loss due to line radiation from heavy impurities is typically similar in magnitude to the energy loss due to bremsstrahlung [14,35].
As before, the heating power per unit volume due to
nuclear fusion reactions is