Next: Fluid Theory Up: Plasma Fluid Theory Previous: Introduction Contents
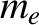 and electrical charge
and electrical charge 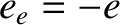 , and ions of mass
, and ions of mass  and electrical charge
and electrical charge 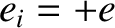 . Note that we are neglecting helium ash particles and
impurity ions, for the sake of simplicity. Assuming that the plasma contains an optimal 50%-50% mixture of
deuterium and tritium ions, it follows that
. Note that we are neglecting helium ash particles and
impurity ions, for the sake of simplicity. Assuming that the plasma contains an optimal 50%-50% mixture of
deuterium and tritium ions, it follows that
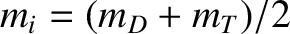 , where
, where 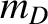 and
and 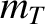 are the deuteron and
triton masses, respectively.
are the deuteron and
triton masses, respectively.
At the most fundamental level, the dynamics of each plasma species is governed by the kinetic equation [18]:
Here,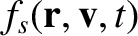 is the ensemble-averaged phase-space density of plasma species
is the ensemble-averaged phase-space density of plasma species  (
( stands for either
stands for either 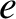 or
or  ) near point
) near point
 at time
at time  , where
, where 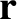 denotes spatial position and
denotes spatial position and 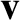 denotes velocity [41]. Moreover,
denotes velocity [41]. Moreover,  and
and 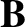 are the ensemble-averaged electric and
magnetic field-strengths, respectively. Finally,
are the ensemble-averaged electric and
magnetic field-strengths, respectively. Finally,
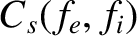 is the collision operator for plasma species
is the collision operator for plasma species  [18].
The electron and ion kinetic equations form a complete set when combined with Maxwell's equations.
[18].
The electron and ion kinetic equations form a complete set when combined with Maxwell's equations.
Equation (2.1) describes plasma dynamics in a six-dimensional space (three spatial dimensions, and three velocity-space dimensions); as such, it is extremely difficult equation to solve. For dynamics that takes place on timescales that are long compared to the inverse ion gyro-frequency, which certainly applies to tearing mode dynamics in tokamak plasmas, the equation can be simplified by averaging over the gyro-motions of charged particles [7,9,25]. The resulting gyro-kinetic equation is only five-dimensional (three spatial dimensions, and two velocity-space dimensions). The electron and ion gyro-kinetic equations have been used extensively to numerically model plasma turbulence in tokamaks [23,39,50]. It turns out that this is possible because turbulent eddies are localized on toroidal magnetic flux-surfaces in flux-tubes that run parallel to the magnetic field and whose radial extents are, at most, a few ion gyro-radii. Moreover, the eddies attain a quasi-steady-state in a matter of a few milliseconds. Hence, despite the high dimensionalities of the gyro-kinetic equations, it is practical to solve them in calculations that only simulate a small fraction of the plasma volume over a time interval of a few milliseconds. Now, tearing modes are global plasma instabilities that evolve on timescales that are hundreds, if not thousands, of milliseconds. Unfortunately, it is simply not practical to simulate the whole plasma over a time interval of a few hundred to a few thousand milliseconds using the gyro-kinetic equations. Hence, a different approach is needed to describe tearing mode dynamics. In fact, the only practical option is to employ fluid theory.