As is well known, the smallness of the toroidal magnetization parameter,  , ensures that the dominant parallel
viscosity tensors,
, ensures that the dominant parallel
viscosity tensors,

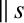 and
and

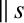 , take the so-called Chew-Goldberger-Low forms [11,29]:
where
, take the so-called Chew-Goldberger-Low forms [11,29]:
where
 . Incidentally, it is clear from Equation (2.60) that the parallel viscosity tensor in the classical closure scheme does indeed take this form.
. Incidentally, it is clear from Equation (2.60) that the parallel viscosity tensor in the classical closure scheme does indeed take this form.
Now, if

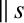 takes the Chew-Goldberger-Low form then
takes the Chew-Goldberger-Low form then
These results follow because
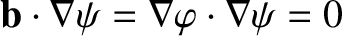 .
.
Furthermore,
where, in Cartesian coordinates,
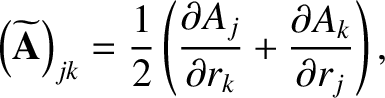 |
(2.157) |
and use has been made of the fact that

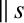 is a symmetric tensor. In fact, it can be shown that [19]
is a symmetric tensor. In fact, it can be shown that [19]
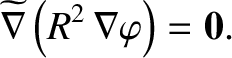 |
(2.158) |
Hence, we deduce that
Making use of Equation (2.150), we obtain
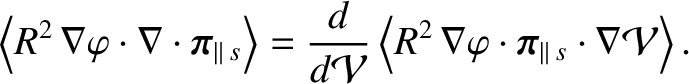 |
(2.160) |
However, if

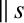 takes the Chew-Goldberger-Low form then
takes the Chew-Goldberger-Low form then


 ,
because
,
because
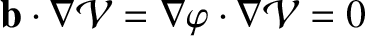 . It follows that [32,34]
. It follows that [32,34]
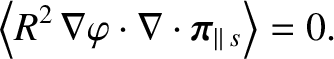 |
(2.161) |
Likewise, if

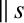 takes the Chew-Goldberger-Low form then
takes the Chew-Goldberger-Low form then
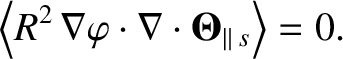 |
(2.162) |
 , ensures that the dominant parallel
viscosity tensors,
, ensures that the dominant parallel
viscosity tensors,

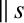 and
and

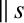 , take the so-called Chew-Goldberger-Low forms [11,29]:
where
, take the so-called Chew-Goldberger-Low forms [11,29]:
where
 . Incidentally, it is clear from Equation (2.60) that the parallel viscosity tensor in the classical closure scheme does indeed take this form.
. Incidentally, it is clear from Equation (2.60) that the parallel viscosity tensor in the classical closure scheme does indeed take this form.

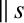 takes the Chew-Goldberger-Low form then
takes the Chew-Goldberger-Low form then
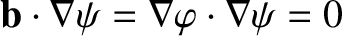 .
.
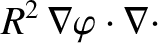
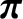
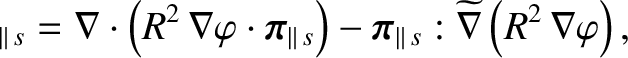
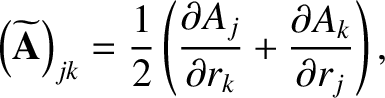

 is a symmetric tensor. In fact, it can be shown that [19]
is a symmetric tensor. In fact, it can be shown that [19]
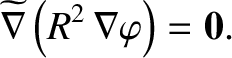
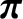
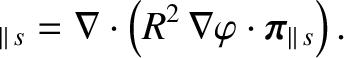

 takes the Chew-Goldberger-Low form then
takes the Chew-Goldberger-Low form then


 ,
because
,
because
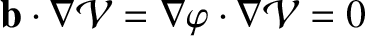 . It follows that [32,34]
Likewise, if
. It follows that [32,34]
Likewise, if

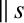 takes the Chew-Goldberger-Low form then
takes the Chew-Goldberger-Low form then