Next: Chew-Goldberger-Low Forms Up: Plasma Fluid Theory Previous: Lowest-Order Flows Contents
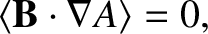 |
(2.149) |
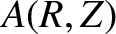 is a general axisymmetric scalar field. Moreover,
is a general axisymmetric scalar field. Moreover,
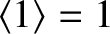 .
.
Making use of Equations (2.121)–(2.123) and (2.129), it is easily demonstrated that
where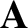 is a general axisymmetric (i.e.,
is a general axisymmetric (i.e.,
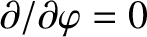 ) vector field, and
) vector field, and
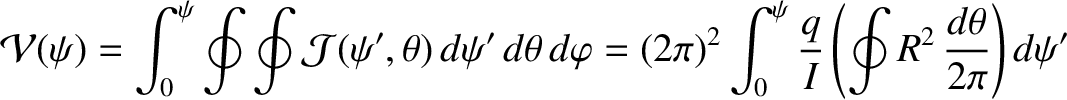 |
(2.151) |
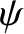 .
.