Next: Friction Force Densities Up: Plasma Fluid Theory Previous: Parallel Flows Contents
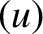 represents a
represents a 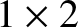 vector, whereas
vector, whereas ![$[A]$](img943.png) represents a
represents a 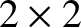 matrix. The elements of
matrix. The elements of
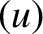 and
and
![$[A]$](img943.png) are denoted
are denoted 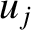 and
and  , respectively, where
, respectively, where 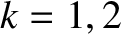 indexes the rows, and
indexes the rows, and 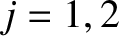 indexes the columns.
Furthermore,
indexes the columns.
Furthermore,  denotes a null vector, and
denotes a null vector, and ![$[1]$](img949.png) denotes an identity matrix.
denotes an identity matrix.
Equations (2.175) and (2.176) can be written in the compact form [38]
where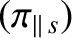 |
![$\displaystyle = \left(\begin{array}{c}\mbox{\boldmath$\pi$}_{\parallel\,s}\\ [0.5ex]\mbox{\boldmath$\Theta$}_{\parallel\,s}\end{array}\right),$](img952.png) |
(2.178) |
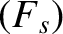 |
![$\displaystyle = \left(\begin{array}{c}{\bf F}_{s\,1}\\ [0.5ex]{\bf F}_{s\,2}\end{array}\right),$](img954.png) |
(2.179) |
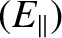 |
![$\displaystyle = \left(\begin{array}{c}\langle {\bf E}\cdot{\bf B}\rangle/\langle B\rangle\\ [0.5ex] 0
\end{array}\right).$](img956.png) |
(2.180) |
It is helpful to define
Equations (2.170)–(2.174), (2.181), and (2.182) can be combined to give where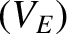 |
![$\displaystyle = \left(\begin{array}{c}
V_{E\,1}\\ [0.5ex]
0
\end{array}\right),$](img963.png) |
(2.184) |
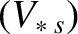 |
![$\displaystyle = \left(\begin{array}{c}
V_{\ast\,s\,1}\\ [0.5ex]
V_{\ast\,s\,2}
\end{array}\right).$](img965.png) |
(2.185) |
It is also helpful to define
It follows from Equations (2.130), (2.134)–(2.137), (2.165), (2.166), and (2.171)–(2.174) that![$\displaystyle (u_{\varphi\,s}) = \frac{I^{\,2}}{\langle R^2\rangle}\left(\begin...
...{\vert\nabla\psi\vert^{\,2}}{B^2}\right\rangle\left[(V_E)+(V_{\ast\,s})\right].$](img967.png) |
(2.187) |
![$\displaystyle \left(\begin{array}{c}\langle
u_{\parallel\,s\,1}/B\rangle\\ [0.5...
...theta) + \left\langle\frac{1}{B^2}\right\rangle\left[(V_E)+(V_{\ast\,s})\right]$](img968.png) |
(2.188) |