Next: Parallel Current Density Up: Plasma Fluid Theory Previous: Determination of Ion Flows Contents
![$\displaystyle ([F_{ee}]+f_t\,[\mu_e])\,(u_{\theta\,e})$](img1063.png) |
![$\displaystyle = (-[F_{ee}]+[F_{ei}])\,(V_E) - [F_{ee}]\,(V_{\ast\,e}) + [F_{ei}]\,\{(u_{\theta\,i})+(V_{\ast\,i})\}$](img1064.png) |
|
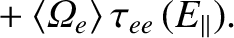 |
(2.234) |
![$(-[F_{ee}]+[F_{ei}])\,(V_E)=(0)$](img1066.png) because
because
 , for
, for 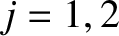 , and
, and
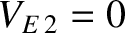 . Hence, we
get
. Hence, we
get
![$\displaystyle ([F_{ee}]+f_t\,[\mu_e])\,(u_{\theta\,e})$](img1063.png) |
![$\displaystyle =- [F_{ee}]\,(V_{\ast\,e}) + [F_{ei}]\,([1]-[L_{ii}])\,(V_{\ast\,i})
+ \langle{\mit\Omega}_{e}\rangle\,\tau_{ee}\,(E_\parallel),$](img1067.png) |
(2.235) |
![$\displaystyle [L_{ee}]$](img1069.png) |
![$\displaystyle = ([F_{ee}] + f_t\,[\mu_e])^{-1}\,[F_{ee}],$](img1070.png) |
(2.237) |
![$\displaystyle [L_{ei}]$](img1071.png) |
![$\displaystyle = ([F_{ee} ]+ f_t\,[\mu_e])^{-1}\,[F_{ei}]\,([1] - [L_{ii}]),$](img1072.png) |
(2.238) |
![$\displaystyle [Q_{ee}]$](img1073.png) |
![$\displaystyle = ([F_{ee}] + f_t\,[\mu_e])^{-1}.$](img1074.png) |
(2.239) |
Making use of Equations (2.197), (2.198), and (2.216), and only retaining terms up to first order in the
small parameter 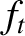 , we get
, we get
It follows from Equations (2.165), (2.166), (2.170), (2.181)–(2.185), (2.236), and (2.240)–(2.242) that
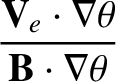 |
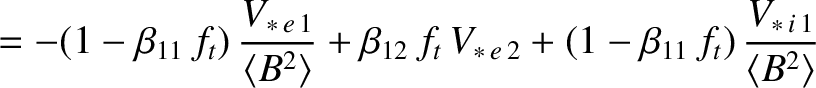 |
|
![$\displaystyle \phantom{=} +\alpha_1\, [1-(\alpha_2+\beta_{11})\,f_t]\,\frac{V_{...
...elta_{11}\,f_t)\,\frac{\langle {\bf E}\cdot{\bf B}\rangle}{\langle B^2\rangle},$](img1103.png) |
(2.255) | |
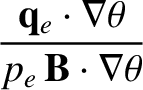 |
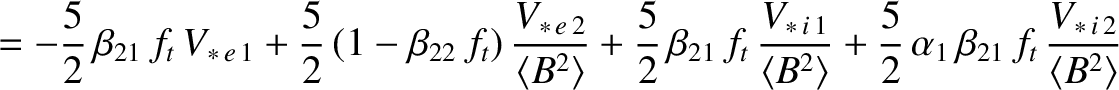 |
|
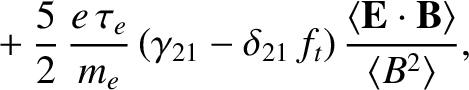 |
(2.256) |
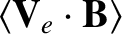 |
 |
|
![$\displaystyle \phantom{=} + \alpha_1\,[1-(\alpha_2+\beta_{11})\,f_t]\,V_{\ast\,...
..._{e}}{m_e}\,(\gamma_{11}-\delta_{11}\,f_t)\,\langle {\bf E}\cdot{\bf B}\rangle,$](img1109.png) |
(2.257) | |
 |
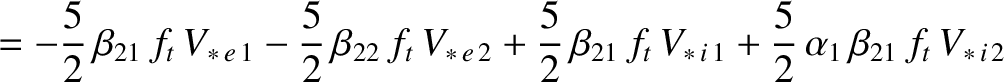 |
|
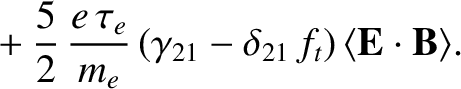 |
(2.258) |
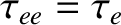 .
.
In the circular magnetic flux-surface limit, Equations (2.255) and (2.256) reduce to
whereas Equations (2.257)–(2.258) yield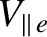 |
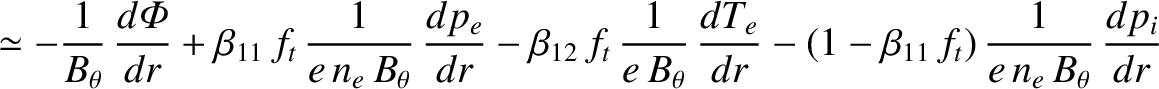 |
|
![$\displaystyle \phantom{=} +\alpha_1\, [1-(\alpha_2+\beta_{11})\,f_t]\,\frac{1}{...
..._i}{dr}-\frac{e\,\tau_{e}}{m_e}\,(\gamma_{11}-\delta_{11}\,f_t)\,E_{\parallel},$](img1121.png) |
(2.261) | |
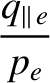 |
 |
|
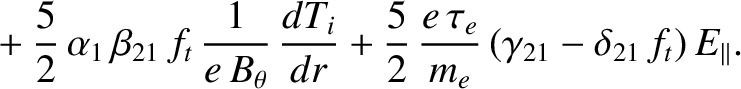 |
(2.262) |
Expressions (2.259)–(2.262) have many features in common with the corresponding expressions, (2.226)–(2.229), for the ions, despite being much more complicated in nature. In particular, the
E-cross-B velocity makes no contribution to the poloidal component of the electron fluid velocity. Moreover, the
poloidal component of the electron fluid velocity is similar in magnitude to a diamagnetic velocity, whereas the
parallel component is larger by a factor
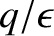 .
.