Next: Neoclassical Transport Up: Plasma Fluid Theory Previous: Determination of Electron Flows Contents
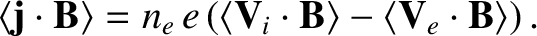 |
(2.263) |
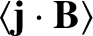 |
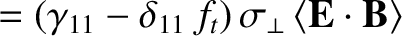 |
|
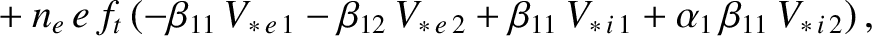 |
(2.264) |
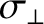 is specified in Equation (2.41).
In the circular magnetic flux-surface limit, the previous expression reduces to [30,52]
where
is specified in Equation (2.41).
In the circular magnetic flux-surface limit, the previous expression reduces to [30,52]
where
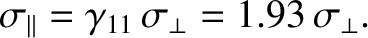 |
(2.266) |
The first term on the right-hand side of Equation (2.265) represents the conventional ohmic parallel current driven by the
inductive parallel electric field. Note, however, that the ohmic current is smaller than that predicted by
the classical fluid closure scheme (see Section 2.6) by a factor
 [33]. The explanation for
this reduction is that trapped electrons cannot carry a net parallel current, because they are forced to periodically
reverse their drift direction parallel to the magnetic field. Hence, the parallel electrical conductivity of the plasma is reduced by a factor that is
roughly equal to the fraction of passing particles [32]. [See Equation (2.201).] This effect
is known as the neoclassical enhancement of (parallel) electrical resistivity, and has been observed in
experiments [15,37,56].
[33]. The explanation for
this reduction is that trapped electrons cannot carry a net parallel current, because they are forced to periodically
reverse their drift direction parallel to the magnetic field. Hence, the parallel electrical conductivity of the plasma is reduced by a factor that is
roughly equal to the fraction of passing particles [32]. [See Equation (2.201).] This effect
is known as the neoclassical enhancement of (parallel) electrical resistivity, and has been observed in
experiments [15,37,56].
The second term on the right-hand side of Equation (2.265) represents a non-inductive parallel current driven by
equilibrium density and temperature gradients that is known as the bootstrap current [5]. The
bootstrap current has also been observed in experiments [54,55]. The ultimate origin of the bootstrap
current is collisional friction between trapped and passing particles. It is, therefore, not surprising that the
current is proportional to the fraction of trapped particles, 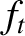 .
.