Next: Island Rotation Frequency Up: Nonlinear Tearing Mode Stability Previous: Composite Linear/Nonlinear Model Contents
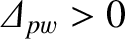 then the width of the magnetic island chain
grows without limit. In fact, this is not the case. Instead, the width of the island chain eventually stops growing, and the
tearing mode attains a saturated steady state. In order to model this effect, it is necessary to perform the
asymptotic matching between the inner and outer regions (see Sections 3.8 and 4.1) to higher order, taking into account the finite
width of the island chain [5,12,15,18].
then the width of the magnetic island chain
grows without limit. In fact, this is not the case. Instead, the width of the island chain eventually stops growing, and the
tearing mode attains a saturated steady state. In order to model this effect, it is necessary to perform the
asymptotic matching between the inner and outer regions (see Sections 3.8 and 4.1) to higher order, taking into account the finite
width of the island chain [5,12,15,18].
For the case of an island chain that is sufficiently wide to flatten the plasma pressure within its magnetic separatrix [6], the appropriate saturation theory is given in Hastie, et alia [9].
According to this theory,
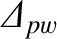 in Equation (9.5) must be replaced by
in Equation (9.5) must be replaced by
 denotes the zero-island-width, perfect-wall, tearing stability index,
Here,
denotes the zero-island-width, perfect-wall, tearing stability index,
Here,  is a radial coordinate in cylindrical geometry,
is a radial coordinate in cylindrical geometry, 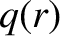 the safety-factor profile (see Section 3.2),
the safety-factor profile (see Section 3.2),
 the equilibrium toroidal current density,
the equilibrium toroidal current density,  the simulated major radius of the plasma,
the simulated major radius of the plasma, 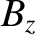 the equilibrium toroidal
magnetic field-strength, and
the equilibrium toroidal
magnetic field-strength, and 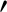 denotes
denotes 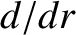 .
.
![\includegraphics[width=0.95\textwidth]{Chapter09/Figure9_2.eps}](img2980.png) |
Equations (9.5) and (9.15) can be combined to give
If we define then Equation (9.20) reduces to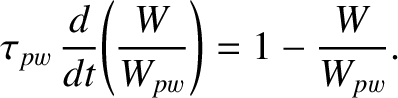 |
(9.23) |
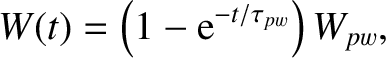 |
(9.24) |
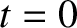 . It follows that the width of the island chain does not grow without limit,
but instead eventually attains the saturated
value
. It follows that the width of the island chain does not grow without limit,
but instead eventually attains the saturated
value
 . Moreover, the time required to achieve saturation,
. Moreover, the time required to achieve saturation, 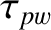 , is of order
, is of order
 .
.
Figure 9.2 shows the saturated island width of an 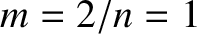 tearing mode, which is
generally the most unstable tearing mode in a conventional tokamak plasma [16], in a so-called “Wesson” equilibrium [16] characterized by
tearing mode, which is
generally the most unstable tearing mode in a conventional tokamak plasma [16], in a so-called “Wesson” equilibrium [16] characterized by
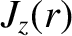 |
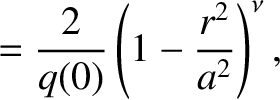 |
(9.25) |
 |
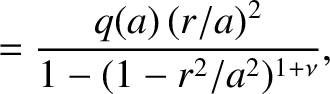 |
(9.26) |
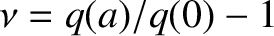 . Here,
. Here, 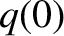 and
and 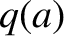 are the safety-factor values at the magnetic axis,
are the safety-factor values at the magnetic axis,  , and the plasma
boundary,
, and the plasma
boundary,  , respectively. In the calculation shown in Figure 9.2,
, respectively. In the calculation shown in Figure 9.2,
 is determined by solving the cylindrical tearing mode
equation, subject to suitable boundary conditions, as described in Section 3.8. Moreover,
is determined by solving the cylindrical tearing mode
equation, subject to suitable boundary conditions, as described in Section 3.8. Moreover, 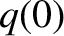 is given the plausible value 0.8 [17], while
is given the plausible value 0.8 [17], while
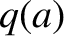 is varied in order to shift the position of the rational surface within the plasma. It can be seen that if the rational
surface lies well inside the plasma boundary then the 2/1 island chain saturates at relatively small width (i.e.,
is varied in order to shift the position of the rational surface within the plasma. It can be seen that if the rational
surface lies well inside the plasma boundary then the 2/1 island chain saturates at relatively small width (i.e.,
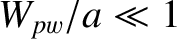 ).
On the other hand, if the rational surface lies close to the plasma boundary then the island chain
saturates at a much higher width. However, the presence of a close-fitting perfectly conducting wall can mitigate this
effect to some extent.
).
On the other hand, if the rational surface lies close to the plasma boundary then the island chain
saturates at a much higher width. However, the presence of a close-fitting perfectly conducting wall can mitigate this
effect to some extent.
Given that the minor radius, 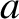 , of a tokamak fusion reactor is a few meters (see Table 1.2), whereas the
typical linear layer width is a few millimeters (see Table 6.2), it is clear from Figure 9.2 that the saturated island
width of an unstable tearing mode in a tokamak fusion reactor is bound to be very much larger than the linear layer width. Thus, we conclude that the time evolution of an unstable tearing mode in such a reactor
will only be governed by linear theory for a comparatively short period of time after its onset, its subsequent time evolution
being governed by nonlinear theory. Furthermore, it will take a time of order the resistive diffusion time,
, of a tokamak fusion reactor is a few meters (see Table 1.2), whereas the
typical linear layer width is a few millimeters (see Table 6.2), it is clear from Figure 9.2 that the saturated island
width of an unstable tearing mode in a tokamak fusion reactor is bound to be very much larger than the linear layer width. Thus, we conclude that the time evolution of an unstable tearing mode in such a reactor
will only be governed by linear theory for a comparatively short period of time after its onset, its subsequent time evolution
being governed by nonlinear theory. Furthermore, it will take a time of order the resistive diffusion time,  , for the
mode to attain its final saturated amplitude.
, for the
mode to attain its final saturated amplitude.
Note, finally, that a saturated magnetic island chain degrades the overall energy confinement properties of a tokamak
plasma because it flattens the pressure profile within its magnetic
separatrix (see Chapter 8 and Section 14.18) [6]. Moreover, the degree of degradation is roughly proportional to  [2].
[2].
![\includegraphics[width=\textwidth]{Chapter09/Figure9_3.eps}](img2999.png) |