Next: Numerical Solution of Resonant Up: Linear Tearing Mode Stability Previous: Linear Growth-Rate Regimes Contents
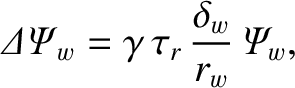 |
(6.23) |
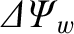 is a measure of the current flowing in the wall,
is a measure of the current flowing in the wall,
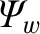 the perturbed magnetic
flux that penetrates the wall,
the perturbed magnetic
flux that penetrates the wall, 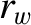 the wall minor radius,
the wall minor radius, 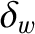 the wall radial thickness, and
the wall radial thickness, and
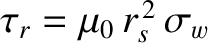 the time required for magnetic flux to diffuse a distance
the time required for magnetic flux to diffuse a distance 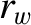 through the wall
material. Here,
through the wall
material. Here,  is the electrical conductivity of the wall material. By analogy with the previous result,
we would expect the dispersion relation of a magnetic perturbation interacting with the thin resistive layer that
surrounds the rational surface to take the form
is the electrical conductivity of the wall material. By analogy with the previous result,
we would expect the dispersion relation of a magnetic perturbation interacting with the thin resistive layer that
surrounds the rational surface to take the form
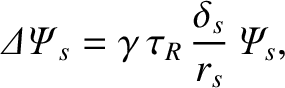 |
(6.24) |
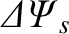 is a measure of the current flowing in the layer,
is a measure of the current flowing in the layer,
 the perturbed magnetic
flux that penetrates the layer,
the perturbed magnetic
flux that penetrates the layer,  is the radial thickness of the layer, and
is the radial thickness of the layer, and  is the time required for magnetic flux to diffuse a distance
is the time required for magnetic flux to diffuse a distance 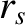 through the plasma. [See Equation (5.49).] Note that, in general,
through the plasma. [See Equation (5.49).] Note that, in general,  is a complex quantity. In fact, the true layer thickness is
is a complex quantity. In fact, the true layer thickness is
 . It follows from Equation (3.74) that
where
. It follows from Equation (3.74) that
where 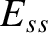 is the real tearing stability index. Finally, Equations (5.48), (5.66), (6.2), and (6.4) can be combined with the previous equation to give
where
is the real tearing stability index. Finally, Equations (5.48), (5.66), (6.2), and (6.4) can be combined with the previous equation to give
where 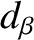 is the ion sound radius at the rational surface. [See Equation (4.75).]
is the ion sound radius at the rational surface. [See Equation (4.75).]