Next: Resistive Layer Physics Up: Cylindrical Tearing Mode Theory Previous: Solution in Presence of Contents
 |
(3.91) |
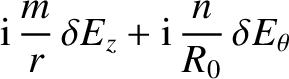 |
 |
(3.92) |
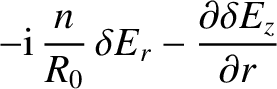 |
 |
(3.93) |
 |
 |
(3.94) |
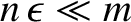 , the previous three equations imply that
where
, the previous three equations imply that
where
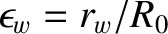 .
Here, we have assumed that
.
Here, we have assumed that
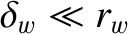 , where
, where 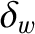 is the radial thickness of the wall. We have
also made use of the fact that
is the radial thickness of the wall. We have
also made use of the fact that
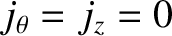 outside the plasma.
outside the plasma.
Inside the wall,
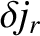 |
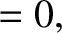 |
(3.98) |
 |
 |
(3.99) |
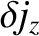 |
 |
(3.100) |
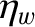 is the wall's electrical resistivity.
Making use of Equations (3.37), (3.38), (3.96), and (3.97), as well as the fact that
is the wall's electrical resistivity.
Making use of Equations (3.37), (3.38), (3.96), and (3.97), as well as the fact that
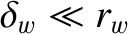 , both of the previous two equations reduce to
Let us adopt the so-called thin-wall limit, according to which
, both of the previous two equations reduce to
Let us adopt the so-called thin-wall limit, according to which
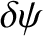 is assumed to vary
only weakly in
is assumed to vary
only weakly in  across the wall. In this limit, integration of the previous equation across the wall yields
where
is the so-called wall time-constant [4,9]. Here, use has been made of Equations (3.82) and (3.83).
The thin-wall limit is
valid as long as the wall thickness is less than the resistive skin depth in the wall material. In other words, provided
that
across the wall. In this limit, integration of the previous equation across the wall yields
where
is the so-called wall time-constant [4,9]. Here, use has been made of Equations (3.82) and (3.83).
The thin-wall limit is
valid as long as the wall thickness is less than the resistive skin depth in the wall material. In other words, provided
that
In the thin wall limit, Equations (3.82) and (3.95)–(3.100) yield
inside the wall. Note that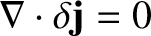 , as is required by charge conservation.
, as is required by charge conservation.