Next: Resistive Wall Physics Up: Cylindrical Tearing Mode Theory Previous: Solution in Presence of Contents
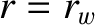 possesses non-zero electrical resistivity, but is surrounded by a perfectly conducting wall
located at radius
possesses non-zero electrical resistivity, but is surrounded by a perfectly conducting wall
located at radius 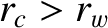 .
The most general solution to the cylindrical tearing mode equation, (3.60), in the outer region can be written
where the real function
.
The most general solution to the cylindrical tearing mode equation, (3.60), in the outer region can be written
where the real function
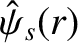 is specified in Section 3.8, and the real function
is specified in Section 3.8, and the real function
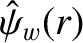 is a solution of
that satisfies
Again, Equation (3.80) ensures that the perturbed magnetic field associated with the tearing mode cannot penetrate the
perfectly conducting wall.
It is easily seen that
is a solution of
that satisfies
Again, Equation (3.80) ensures that the perturbed magnetic field associated with the tearing mode cannot penetrate the
perfectly conducting wall.
It is easily seen that
In general,
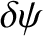 is continuous across the resistive wall (in accordance with Maxwell's equations), whereas
is continuous across the resistive wall (in accordance with Maxwell's equations), whereas
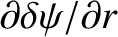 is discontinuous. The discontinuity in
is discontinuous. The discontinuity in
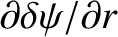 is caused by a helical current sheet induced in the wall. The complex quantity
is caused by a helical current sheet induced in the wall. The complex quantity
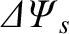 |
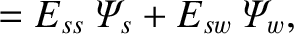 |
(3.84) |
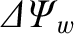 |
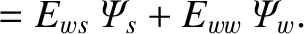 |
(3.85) |
Equations (3.64) and (3.77) can be combined to give
 |
(3.89) |
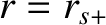 to
to  , making use of Equations (3.66), (3.67), (3.78), (3.79), (3.87),
and (3.88), then we obtain [4]
, making use of Equations (3.66), (3.67), (3.78), (3.79), (3.87),
and (3.88), then we obtain [4]