Cylindrical Tearing Mode Equation
The magnetic structure of a tearing perturbation is determined by the so-called cylindrical tearing mode equation, (3.35), which can be written in the form [4,14]
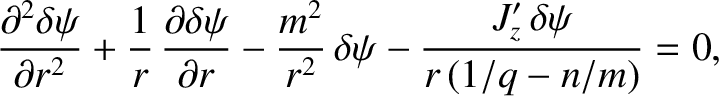 |
(3.60) |
where
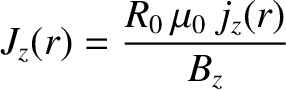 |
(3.61) |
is a dimensionless measure of the toroidal current density profile.
Note that Equation (3.60) is singular at the so-called rational magnetic flux-surface, radius  , at which
, at which
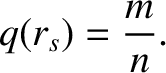 |
(3.62) |
At the rational surface,
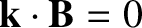 , where
, where  is the equilibrium magnetic field, and
is the equilibrium magnetic field, and
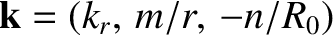 the wavevector of the tearing perturbation.
the wavevector of the tearing perturbation.
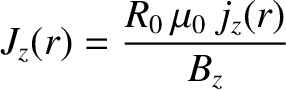
 , at which
At the rational surface,
, at which
At the rational surface,
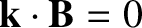 , where
, where 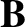 is the equilibrium magnetic field, and
is the equilibrium magnetic field, and
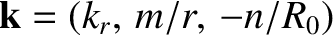 the wavevector of the tearing perturbation.
the wavevector of the tearing perturbation.