Next: Cylindrical Tearing Mode Equation Up: Cylindrical Tearing Mode Theory Previous: Fluid Continuity Contents
 |
(3.55) |
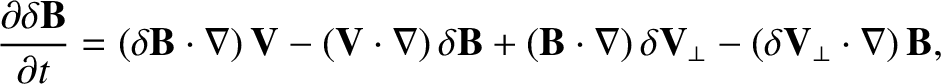 |
(3.56) |
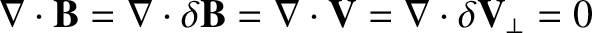 .
The radial component of the previous equation yields
where use has been made of Equations (3.9), (3.19), (3.32), (3.52), and (3.53).
Equations (3.54) and (3.58) imply that
Hence, we deduce that the perturbed plasma flow associated with a tearing mode in a low-
.
The radial component of the previous equation yields
where use has been made of Equations (3.9), (3.19), (3.32), (3.52), and (3.53).
Equations (3.54) and (3.58) imply that
Hence, we deduce that the perturbed plasma flow associated with a tearing mode in a low-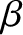 , large aspect-ratio, tokamak plasma is divergence-free [see Equations (3.51) and (3.59)], and is specified by Equations (3.57) and (3.58).
, large aspect-ratio, tokamak plasma is divergence-free [see Equations (3.51) and (3.59)], and is specified by Equations (3.57) and (3.58).