Next: Velocity Perturbation Up: Cylindrical Tearing Mode Theory Previous: Density and Temperature Perturbations Contents
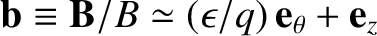 . It follows that
. It follows that
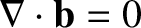 and
and
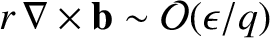 .
Thus,
where use has been made of Equation (3.29).
.
Thus,
where use has been made of Equation (3.29).
Now, the equilibrium plasma flow is written
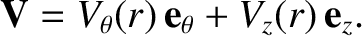 |
(3.47) |
The linearized form of Equation (3.45) is
where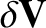 is the perturbed plasma velocity, and use has been made of Equations (3.46) and (3.48). Let us write
It follows that
where use has been made of Equations (3.8) and (3.19).
Hence,
writing
Equation (3.49) reduces to
where use has been made of Equation (3.42).
is the perturbed plasma velocity, and use has been made of Equations (3.46) and (3.48). Let us write
It follows that
where use has been made of Equations (3.8) and (3.19).
Hence,
writing
Equation (3.49) reduces to
where use has been made of Equation (3.42).