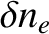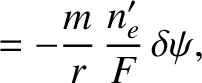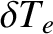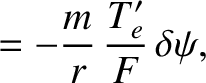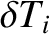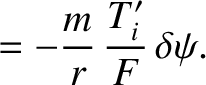According to the equations of marginally-stable ideal-MHD, (2.375)–(2.380), the electron number density, the electron temperature,
and the ion temperature all satisfy equations of the form
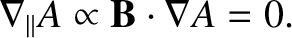 |
(3.39) |
Linearization of the previous equation yields
 |
(3.40) |
where 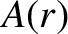 denotes an equilibrium quantity. It follows from Equations (3.8), (3.19), and (3.32) that
denotes an equilibrium quantity. It follows from Equations (3.8), (3.19), and (3.32) that
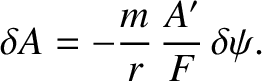 |
(3.41) |
More explicitly, we conclude that the perturbations in the electron number density, the electron temperature,
and the ion temperature that are associated with a tearing mode in a low-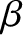 , large aspect-ratio, tokamak plasma take the respective forms
, large aspect-ratio, tokamak plasma take the respective forms
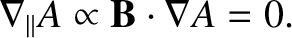

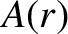 denotes an equilibrium quantity. It follows from Equations (3.8), (3.19), and (3.32) that
denotes an equilibrium quantity. It follows from Equations (3.8), (3.19), and (3.32) that
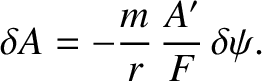
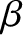 , large aspect-ratio, tokamak plasma take the respective forms
, large aspect-ratio, tokamak plasma take the respective forms