Magnetic Field and Current Density Perturbations
Consider a tearing mode perturbation that has  periods in the poloidal direction,
and
periods in the poloidal direction,
and 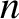 periods in the toroidal direction, where
periods in the toroidal direction, where 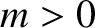 ,
, 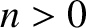 , and
, and
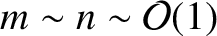 . We shall assume that
all perturbed scalar and vector quantities vary as
respectively,
where
. We shall assume that
all perturbed scalar and vector quantities vary as
respectively,
where
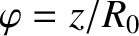 is a simulated toroidal angle.
is a simulated toroidal angle.
Given that tearing modes in tokamak plasmas are relatively low-amplitude (i.e.,
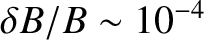 ) [15], global
(i.e.,
) [15], global
(i.e.,
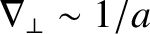 ) [see Equation (2.352)], relatively slowly-growing (i.e.,
) [see Equation (2.352)], relatively slowly-growing (i.e.,
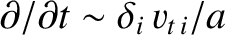 ) [see Equation (2.362)] instabilities, it follows from the analysis of Section 2.25 that they are governed by the linearized forms of the
equations of marginally-stable ideal-MHD, (2.375)–(2.380). In particular, the
linearized form of the curl of the force balance criterion, (2.377), combined with the linearized forms of
Maxwell's equations, (2.349)–(2.351), give
) [see Equation (2.362)] instabilities, it follows from the analysis of Section 2.25 that they are governed by the linearized forms of the
equations of marginally-stable ideal-MHD, (2.375)–(2.380). In particular, the
linearized form of the curl of the force balance criterion, (2.377), combined with the linearized forms of
Maxwell's equations, (2.349)–(2.351), give
where
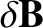 and
and
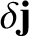 are the perturbed magnetic field and current density, respectively.
are the perturbed magnetic field and current density, respectively.
Equations (3.1), (3.3), and (3.9)–(3.12) yield
and
 |
(3.15) |
with
where
If we write
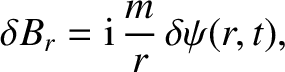 |
(3.20) |
then, after some algebra, Equations (3.13)–(3.17) reduce to
and [6,10]
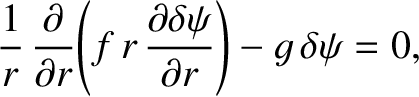 |
(3.23) |
where
Now, a global tearing instability in a low-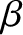 , large aspect-ratio, tokamak plasma is characterized by [6]
, large aspect-ratio, tokamak plasma is characterized by [6]
It follows from Equations (3.4), (3.5), (3.7), and (3.19) that
Thus, in the low-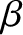 , large aspect-ratio limit, Equations (3.20)–(3.25) simplify considerably to give
and
, large aspect-ratio limit, Equations (3.20)–(3.25) simplify considerably to give
and
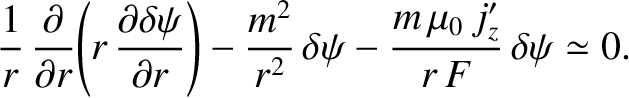 |
(3.35) |
It is also easily demonstrated that
Hence, we conclude that the magnetic field and current density perturbations associated with a
tearing mode in a low-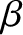 , large aspect-ratio, tokamak plasma are specified by Equations (3.32)–(3.38).
From now on, we shall treat
, large aspect-ratio, tokamak plasma are specified by Equations (3.32)–(3.38).
From now on, we shall treat 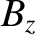 as approximately independent of
as approximately independent of  , in accordance with Equation (3.29).
, in accordance with Equation (3.29).
 periods in the poloidal direction,
and
periods in the poloidal direction,
and 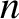 periods in the toroidal direction, where
periods in the toroidal direction, where 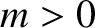 ,
, 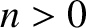 , and
, and
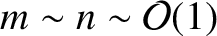 . We shall assume that
all perturbed scalar and vector quantities vary as
respectively,
where
. We shall assume that
all perturbed scalar and vector quantities vary as
respectively,
where
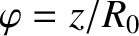 is a simulated toroidal angle.
is a simulated toroidal angle.
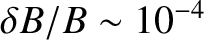 ) [15], global
(i.e.,
) [15], global
(i.e.,
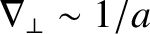 ) [see Equation (2.352)], relatively slowly-growing (i.e.,
) [see Equation (2.352)], relatively slowly-growing (i.e.,
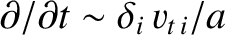 ) [see Equation (2.362)] instabilities, it follows from the analysis of Section 2.25 that they are governed by the linearized forms of the
equations of marginally-stable ideal-MHD, (2.375)–(2.380). In particular, the
linearized form of the curl of the force balance criterion, (2.377), combined with the linearized forms of
Maxwell's equations, (2.349)–(2.351), give
) [see Equation (2.362)] instabilities, it follows from the analysis of Section 2.25 that they are governed by the linearized forms of the
equations of marginally-stable ideal-MHD, (2.375)–(2.380). In particular, the
linearized form of the curl of the force balance criterion, (2.377), combined with the linearized forms of
Maxwell's equations, (2.349)–(2.351), give
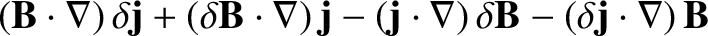
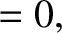

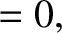
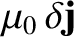
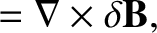
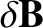 and
and
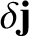 are the perturbed magnetic field and current density, respectively.
are the perturbed magnetic field and current density, respectively.
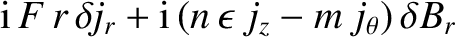
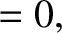
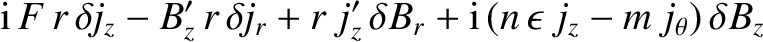
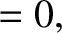

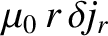
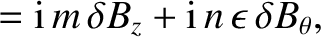
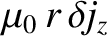

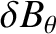
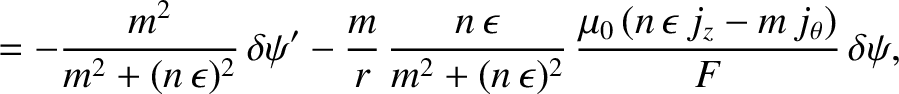
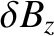

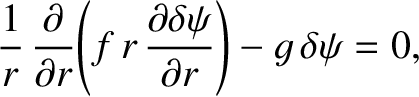

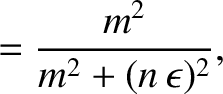
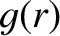
![$\displaystyle =\frac{m}{r}\left\{\frac{m}{r} + \frac{\mu_0\,j_z'}{F} -\left[\fr...
...\,\epsilon)^2}\,\frac{\mu_0\,(n\,\epsilon\,j_z-m\,j_\theta)}{F}\right]' \right.$](img1467.png)
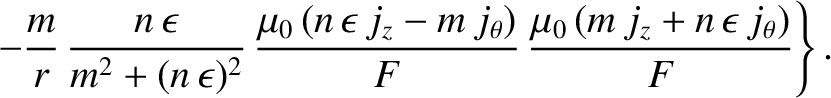
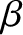 , large aspect-ratio, tokamak plasma is characterized by [6]
, large aspect-ratio, tokamak plasma is characterized by [6]
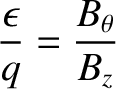
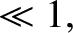
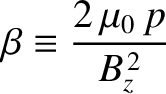
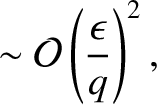


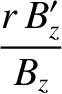
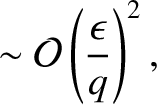

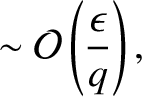
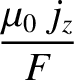
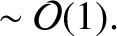
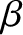 , large aspect-ratio limit, Equations (3.20)–(3.25) simplify considerably to give
and
It is also easily demonstrated that
Hence, we conclude that the magnetic field and current density perturbations associated with a
tearing mode in a low-
, large aspect-ratio limit, Equations (3.20)–(3.25) simplify considerably to give
and
It is also easily demonstrated that
Hence, we conclude that the magnetic field and current density perturbations associated with a
tearing mode in a low-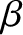 , large aspect-ratio, tokamak plasma are specified by Equations (3.32)–(3.38).
From now on, we shall treat
, large aspect-ratio, tokamak plasma are specified by Equations (3.32)–(3.38).
From now on, we shall treat 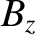 as approximately independent of
as approximately independent of  , in accordance with Equation (3.29).
, in accordance with Equation (3.29).