Next: Magnetic Field and Current Up: Cylindrical Tearing Mode Theory Previous: Introduction Contents
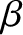 , large aspect-ratio, tokamak plasma equilibrium whose magnetic flux-surfaces map out (almost) concentric circles in the poloidal plane. Such an equilibrium can be approximated as a periodic cylinder [4,14].
Let us employ a conventional set of right-handed cylindrical coordinates,
, large aspect-ratio, tokamak plasma equilibrium whose magnetic flux-surfaces map out (almost) concentric circles in the poloidal plane. Such an equilibrium can be approximated as a periodic cylinder [4,14].
Let us employ a conventional set of right-handed cylindrical coordinates,  ,
,  ,
, 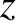 . The
equilibrium magnetic flux-surfaces lie on surfaces of constant
. The
equilibrium magnetic flux-surfaces lie on surfaces of constant  . The system is
assumed to be periodic in the
. The system is
assumed to be periodic in the 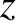 (“toroidal”) direction, with periodicity length
(“toroidal”) direction, with periodicity length 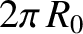 ,
where
,
where  is the simulated major radius of the plasma. Let
is the simulated major radius of the plasma. Let 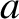 be the minor radius of the plasma. The equilibrium magnetic
field is written
where
be the minor radius of the plasma. The equilibrium magnetic
field is written
where
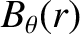 is the poloidal magnetic field-strength, and
is the poloidal magnetic field-strength, and 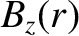 the toroidal magnetic field-strength.
Here,
the toroidal magnetic field-strength.
Here,
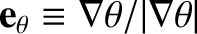 and
and
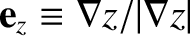 . The safety-factor profile takes the form
[See Equation (1.76).] It is assumed that
. The safety-factor profile takes the form
[See Equation (1.76).] It is assumed that
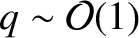 .
The equilibrium current density is written
where
the poloidal and toroidal current densities
take the respective forms
and
.
The equilibrium current density is written
where
the poloidal and toroidal current densities
take the respective forms
and 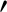 denotes
denotes 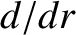 . The plasma equilibrium satisfies the force balance criterion [see Equation (2.377)],
where
. The plasma equilibrium satisfies the force balance criterion [see Equation (2.377)],
where 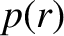 is the total plasma pressure. It follows from Equations (3.1) and (3.3)–(3.5) that
is the total plasma pressure. It follows from Equations (3.1) and (3.3)–(3.5) that