Next: Solution in Presence of Up: Cylindrical Tearing Mode Theory Previous: Cylindrical Tearing Mode Equation Contents
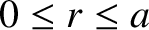 , where
, where 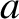 is the plasma minor radius. It follows that
is the plasma minor radius. It follows that
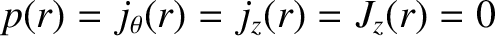 for
for 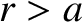 . Let the plasma be surrounded by a concentric, rigid, radially-thin, perfectly conducting wall of radius
. Let the plasma be surrounded by a concentric, rigid, radially-thin, perfectly conducting wall of radius 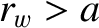 .
(In most circumstances, the wall represents the metallic vacuum vessel that surrounds the plasma.) An appropriate
physical solution of the cylindrical tearing mode equation, (3.60), takes the separable form
where the real function
.
(In most circumstances, the wall represents the metallic vacuum vessel that surrounds the plasma.) An appropriate
physical solution of the cylindrical tearing mode equation, (3.60), takes the separable form
where the real function
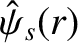 is a solution of
that satisfies
Equation (3.65) ensures that the perturbed magnetic field associated with the tearing mode remains finite at the magnetic axis (
is a solution of
that satisfies
Equation (3.65) ensures that the perturbed magnetic field associated with the tearing mode remains finite at the magnetic axis ( ),
whereas Equation (3.67) represents the physical constraint that the perturbed magnetic field
cannot penetrate a perfectly conducting wall.
),
whereas Equation (3.67) represents the physical constraint that the perturbed magnetic field
cannot penetrate a perfectly conducting wall.
Let
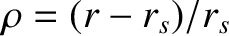 .
The solution of Equation (3.64) in the vicinity of the rational surface is
.
The solution of Equation (3.64) in the vicinity of the rational surface is
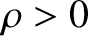 , and
for
, and
for  . Here,
Moreover, the real parameters
. Here,
Moreover, the real parameters
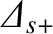 and
and
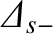 are fully determined by Equation (3.64)
and the boundary conditions (3.65)–(3.67). Note that, in general,
are fully determined by Equation (3.64)
and the boundary conditions (3.65)–(3.67). Note that, in general,
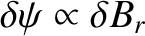 is continuous across the rational surface (in accordance with Maxwell's equations),
whereas
is continuous across the rational surface (in accordance with Maxwell's equations),
whereas
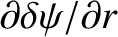 is discontinuous. The discontinuity in
is discontinuous. The discontinuity in
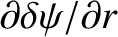 implies the presence of a radially-thin, helical current sheet at the rational surface. This current sheet is resolved in a thin
resistive layer that, in principle, can only be described by employing the full
set of neoclassical fluid equations, (2.370)–(2.374), rather than the reduced set of marginally-stable ideal-MHD equations,
(2.375)–(2.380).
implies the presence of a radially-thin, helical current sheet at the rational surface. This current sheet is resolved in a thin
resistive layer that, in principle, can only be described by employing the full
set of neoclassical fluid equations, (2.370)–(2.374), rather than the reduced set of marginally-stable ideal-MHD equations,
(2.375)–(2.380).
The value of
 at the rational surface,
at the rational surface,
 is, in general, a complex quantity.
The complex quantity
parameterizes the amplitude and phase of the current sheet flowing (parallel to the equilibrium magnetic field) at the rational surface. Asymptotically matching the solutions
in the so-called inner region (i.e., the region of the plasma in the immediate vicinity of the rational surface)
and the so-called outer region (i.e., everywhere in the plasma other than the inner region) with the help
of Equations (3.63), (3.68), (3.69), and (3.73), we obtain
where
is, in general, a complex quantity.
The complex quantity
parameterizes the amplitude and phase of the current sheet flowing (parallel to the equilibrium magnetic field) at the rational surface. Asymptotically matching the solutions
in the so-called inner region (i.e., the region of the plasma in the immediate vicinity of the rational surface)
and the so-called outer region (i.e., everywhere in the plasma other than the inner region) with the help
of Equations (3.63), (3.68), (3.69), and (3.73), we obtain
where
![$\displaystyle E_{ss}= \left[r\,\frac{d\hat{\psi}_s}{dr}\right]_{r_{s-}}^{r_{s+}}={\mit\Delta}_{s+}-{\mit\Delta}_{s-}$](img1555.png) |
(3.75) |