Next: Linear Growth-Rate Regimes Up: Linear Tearing Mode Stability Previous: Linear Dispersion Relation Contents
 space (i.e., Fourier space). The
small-
space (i.e., Fourier space). The
small- layer turns out to be of width
layer turns out to be of width
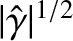 , where
Here,
, where
Here, 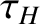 is the hydromagnetic timescale defined in Equation (5.43). Given that we are effectively assuming that
is the hydromagnetic timescale defined in Equation (5.43). Given that we are effectively assuming that
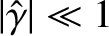 , the condition for the separation of the layer solution into two layers (i.e., that the width of the small-
, the condition for the separation of the layer solution into two layers (i.e., that the width of the small- layer is less than that of the large-
layer is less than that of the large- layer) is always satisfied. The large-
layer) is always satisfied. The large- layer is governed by the equation
where
layer is governed by the equation
where
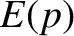 |
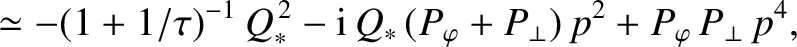 |
(6.6) |
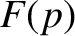 |
 |
(6.7) |
 is the normalized diamagnetic frequency [see Equation (5.65)],
is the normalized diamagnetic frequency [see Equation (5.65)], 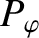 and
and  are magnetic Prandtl numbers [see Equations (5.53) and (5.54)], and
are magnetic Prandtl numbers [see Equations (5.53) and (5.54)], and 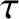 is the ratio of the electron
to the ion pressure gradient at the rational surface [see Equation (4.5)].
The boundary conditions on Equation (6.5) are
that
is the ratio of the electron
to the ion pressure gradient at the rational surface [see Equation (4.5)].
The boundary conditions on Equation (6.5) are
that  is bounded as
is bounded as
 , and
as
, and
as
 . Here,
. Here, 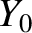 is an arbitrary constant.
is an arbitrary constant.
In the various constant- linear growth-rate regimes considered in the next section, Equation (6.5) reduces to an equation of the form
linear growth-rate regimes considered in the next section, Equation (6.5) reduces to an equation of the form
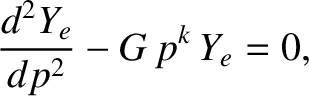 |
(6.9) |
 is real and non-negative, and
is real and non-negative, and 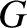 is a complex constant. As described in Section 5.8, the solution of this
equation that is bounded as
is a complex constant. As described in Section 5.8, the solution of this
equation that is bounded as
 can be matched to the small-
can be matched to the small- asymptotic form (6.8) to give
asymptotic form (6.8) to give
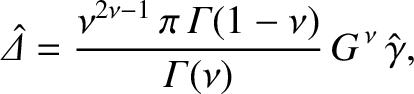 |
(6.10) |
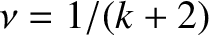 . The width of the large-
. The width of the large- layer in
layer in  space is
space is
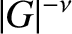 .
.