Next: Nonconstant- Limit Up: Linear Resonant Response Model Previous: Constant- Limit Contents
 Linear Resonant Response Regimes
Linear Resonant Response Regimes
 and
and
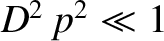 . It follows that
. It follows that 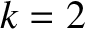 ,
, 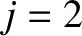 ,
,  , and
, and
![$\displaystyle G = \frac{[-{\rm i}\,(Q-Q_E)]\,[-{\rm i}\,(Q-Q_E-Q_i)]}{-{\rm i}\,(Q-Q_E-\,Q_e)}.$](img2190.png) |
(5.92) |
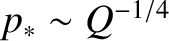 ,
which implies that the regime is valid when
,
which implies that the regime is valid when
 ,
,  ,
, 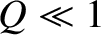 , and
, and
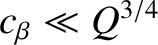 .
.
Suppose that
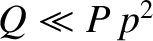 and
and
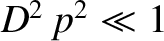 . It follows that
. It follows that  ,
,  ,
,  , and
, and
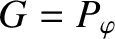 .
Hence, we deduce that
.
Hence, we deduce that
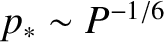 , which implies that
the regime is valid when
, which implies that
the regime is valid when
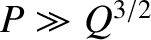 ,
,  ,
,
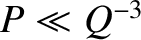 , and
, and
 .
.
Suppose that
 and
and
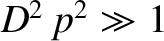 . It follows that
. It follows that  ,
, 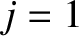 ,
, 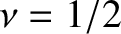 , and
, and
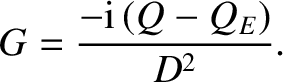 |
(5.95) |
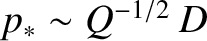 , which implies that the regime is valid when
, which implies that the regime is valid when 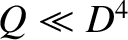 ,
,
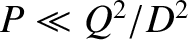 ,
, 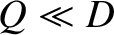 , and
, and
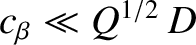 .
.
Suppose, finally, that
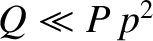 and
and
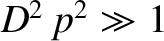 . It follows that
. It follows that 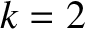 ,
, 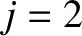 ,
,  , and
, and
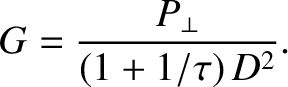 |
(5.97) |
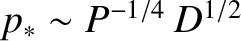 , which implies that the regime is valid when
, which implies that the regime is valid when
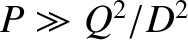 ,
,
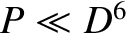 ,
,
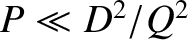 , and
, and
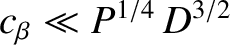 .
.