Nonconstant- Limit
Limit
Suppose that
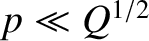 . In this limit, Equation (5.78) reduces to
. In this limit, Equation (5.78) reduces to
![$\displaystyle \frac{d}{dp}\!\left(p^2\,\frac{dY_e}{dp}\right)-[-{\rm i}\,(Q-Q_E-Q_e)]\,\frac{B(p)}{C(p)}\,p^2\,Y_e=0.$](img2227.png) |
(5.99) |
In the various nonconstant- regimes considered in Section 5.11, the previous equation takes the form
regimes considered in Section 5.11, the previous equation takes the form
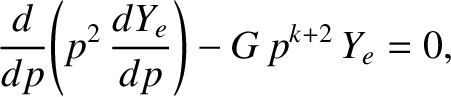 |
(5.100) |
where  is real and non-negative, and
is real and non-negative, and 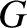 is a complex constant. Let
is a complex constant. Let 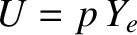 . The previous equation
yields
. The previous equation
yields
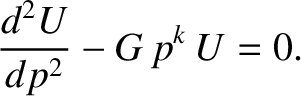 |
(5.101) |
This equation is identical in form to Equation (5.88), which we have already solved. Indeed, the solution that
is bounded as
 has the small-
has the small- expansion (5.90), where
expansion (5.90), where
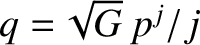 ,
,
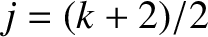 , and
, and
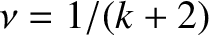 . Matching to Equation (5.83) yields
. Matching to Equation (5.83) yields
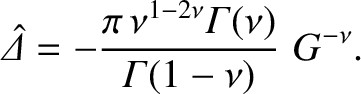 |
(5.102) |
The layer width in  -space again scales as
-space again scales as
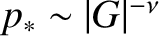 . This width must be
less that
. This width must be
less that 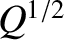 . As before, the neglect of the term involving
. As before, the neglect of the term involving  in Equation (5.74) is
justified provided that
in Equation (5.74) is
justified provided that
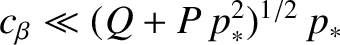 .
.
 Limit
Limit
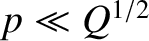 . In this limit, Equation (5.78) reduces to
. In this limit, Equation (5.78) reduces to
![$\displaystyle \frac{d}{dp}\!\left(p^2\,\frac{dY_e}{dp}\right)-[-{\rm i}\,(Q-Q_E-Q_e)]\,\frac{B(p)}{C(p)}\,p^2\,Y_e=0.$](img2227.png)
 regimes considered in Section 5.11, the previous equation takes the form
regimes considered in Section 5.11, the previous equation takes the form
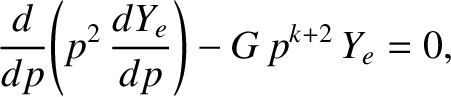
 is real and non-negative, and
is real and non-negative, and 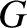 is a complex constant. Let
is a complex constant. Let 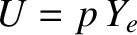 . The previous equation
yields
. The previous equation
yields
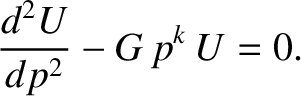
 has the small-
has the small- expansion (5.90), where
expansion (5.90), where
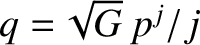 ,
,
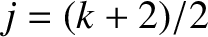 , and
, and
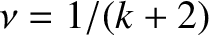 . Matching to Equation (5.83) yields
. Matching to Equation (5.83) yields
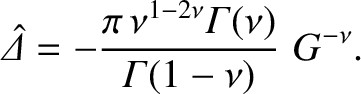
 -space again scales as
-space again scales as
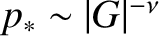 . This width must be
less that
. This width must be
less that 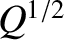 . As before, the neglect of the term involving
. As before, the neglect of the term involving  in Equation (5.74) is
justified provided that
in Equation (5.74) is
justified provided that
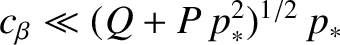 .
.