Next: Constant- Limit Up: Linear Resonant Response Model Previous: Asymptotic Matching Contents
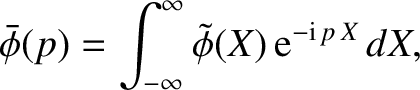 |
(5.72) |
 . Here,
. Here,
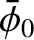 is an arbitrary constant, and use has been made of Equation (5.71).
is an arbitrary constant, and use has been made of Equation (5.71).
In accordance with our previous discussion, we have neglected the parallel transport terms in Equation (5.74).
Let us also ignore the term
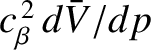 . This approximation can
be justified a posteriori. It is equivalent to the neglect of the contribution of ion parallel dynamics to the linear plasma
response in the resonant layer, and effectively decouples Equation (5.76) from Equations (5.73)–(5.75)
[22]. Equations (5.73)–(5.75) reduce to [7,15]
. This approximation can
be justified a posteriori. It is equivalent to the neglect of the contribution of ion parallel dynamics to the linear plasma
response in the resonant layer, and effectively decouples Equation (5.76) from Equations (5.73)–(5.75)
[22]. Equations (5.73)–(5.75) reduce to [7,15]
 |
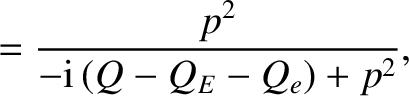 |
(5.79) |
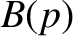 |
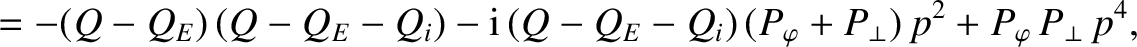 |
(5.80) |
 |
![$\displaystyle =
-{\rm i}\,(Q-Q_E-Q_e) +\left[P_\perp - {\rm i}\,(Q-Q_E-Q_i)\,D^2\right] p^2+(1+1/\tau)\,P_\varphi\,D^2\,p^4,$](img2151.png) |
(5.81) |
 is the normalized, Fourier transformed, electron fluid stream-function. It is easily
demonstrated that
is the normalized, Fourier transformed, electron fluid stream-function. It is easily
demonstrated that
 |
(5.82) |
 .
Hence, the boundary conditions on Equation (5.78) are that
.
Hence, the boundary conditions on Equation (5.78) are that  is bounded as
is bounded as
 , and
as
, and
as
 , where
, where 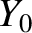 is an arbitrary constant. Here, use has been made of Equation (5.77). In the following, we shall assume that
is an arbitrary constant. Here, use has been made of Equation (5.77). In the following, we shall assume that
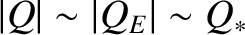 ,
,
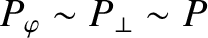 , and
, and
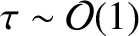 , for the
sake of simplicity.
, for the
sake of simplicity.