Next: Asymptotic Matching Up: Linear Resonant Response Model Previous: Linearized Reduced Drift-MHD Equations Contents
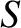 , which is the nominal ratio of the plasma inertia term to the resistive diffusion term in the plasma Ohm's law [14], is very much greater than unity. In fact, according to Table 1.5,
, which is the nominal ratio of the plasma inertia term to the resistive diffusion term in the plasma Ohm's law [14], is very much greater than unity. In fact, according to Table 1.5, 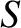 typically exceeds
typically exceeds 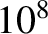 in a tokamak fusion reactor.
However, a resonant layer is
characterized by a balance between plasma inertia and resistive diffusion [17]. Such a balance is
only possible if the layer is very narrow in the radial direction (because a narrow layer enhances radial derivatives, and, thereby, enhances
resistive diffusion). Let us define the stretched radial variable [2]
Assuming that
in a tokamak fusion reactor.
However, a resonant layer is
characterized by a balance between plasma inertia and resistive diffusion [17]. Such a balance is
only possible if the layer is very narrow in the radial direction (because a narrow layer enhances radial derivatives, and, thereby, enhances
resistive diffusion). Let us define the stretched radial variable [2]
Assuming that
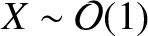 in the layer (i.e., assuming that the layer thickness is roughly of order
in the layer (i.e., assuming that the layer thickness is roughly of order
 ),
and making use of the fact that
),
and making use of the fact that 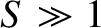 , we deduce that
, we deduce that
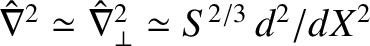 .
Hence, the linear equations (5.39)–(5.42) reduce to the following set of resonant layer equations [7,15]:
Here,
.
Hence, the linear equations (5.39)–(5.42) reduce to the following set of resonant layer equations [7,15]:
Here,
Table 5.1 gives estimates for the values of the dimensionless parameters that characterize the resonant layer equations, (5.57)–(5.60), in a low-field
and a high-field tokamak fusion reactor. (See Chapter 1.) These estimates are made using the following assumptions:
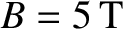 (low-field) or
(low-field) or
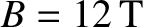 (high-field),
(high-field),
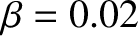 ,
,
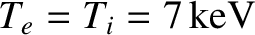 ,
,
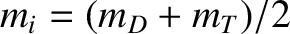 (where
(where 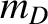 and
and 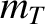 are the deuteron and triton masses, respectively),
are the deuteron and triton masses, respectively),
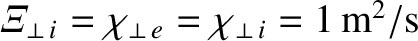 ,
, 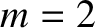 ,
,  ,
, 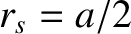 (where
(where 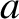 is the minor radius of the plasma),
is the minor radius of the plasma), 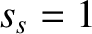 ,
, 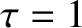 ,
,
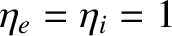 , and
, and
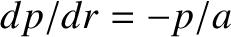 . The parallel energy diffusivities,
. The parallel energy diffusivities,
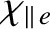 and
and
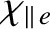 , are estimated from Equations (2.319) and (2.320), respectively,
using
, are estimated from Equations (2.319) and (2.320), respectively,
using
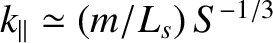 , which is the typical parallel wavenumber of the tearing perturbation at the edge of a resistive layer
whose characteristic thickness is
, which is the typical parallel wavenumber of the tearing perturbation at the edge of a resistive layer
whose characteristic thickness is
 . Note that
. Note that
 , which allows us to neglect the
parallel transport terms (i.e., the terms involving
, which allows us to neglect the
parallel transport terms (i.e., the terms involving
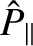 ) in Equation (5.58). The neglect of these terms is justified because the linear layer width is much less than the critical width,
) in Equation (5.58). The neglect of these terms is justified because the linear layer width is much less than the critical width,