Next: Resonant Layer Equations Up: Linear Resonant Response Model Previous: Plasma Equilibrium Contents
 , and
, and 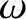 is the rotation frequency of the tearing perturbation in the laboratory frame.
Here,
is the rotation frequency of the tearing perturbation in the laboratory frame.
Here,  denotes a perturbed quantity.
Substituting Equations (5.33)–(5.38) into the reduced drift-MHD model, (5.8)–(5.13), and only retaining terms that
are first order in perturbed quantities, we obtain the following set of linear equations:
Here,
is the hydromagnetic time,
the
E-cross-B frequency,
the electron diamagnetic
frequency,
the ion diamagnetic
frequency,
the (total) diamagnetic frequency,
the Lundquist number [note that this is a slightly different definition to that given in Equation (1.84)],
the
resistive diffusion time [note that this is a slightly different definition to that given in Equation (1.83)],
the toroidal momentum confinement time,
the effective parallel energy equilibration time, and
the effective energy confinement time.
Furthermore,
denotes a perturbed quantity.
Substituting Equations (5.33)–(5.38) into the reduced drift-MHD model, (5.8)–(5.13), and only retaining terms that
are first order in perturbed quantities, we obtain the following set of linear equations:
Here,
is the hydromagnetic time,
the
E-cross-B frequency,
the electron diamagnetic
frequency,
the ion diamagnetic
frequency,
the (total) diamagnetic frequency,
the Lundquist number [note that this is a slightly different definition to that given in Equation (1.84)],
the
resistive diffusion time [note that this is a slightly different definition to that given in Equation (1.83)],
the toroidal momentum confinement time,
the effective parallel energy equilibration time, and
the effective energy confinement time.
Furthermore,