Parallel Closure Scheme
There are a number of other terms that appear in the so-called Braginskii equations, described in Section 2.6, that are subject to modification in a long mean-free-path plasma. .
Consider the thermal force density [see Equation (2.36)]:
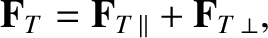 |
(2.305) |
where
Both the parallel and the perpendicular components of this force density are a consequence of the
fact that the friction force density is inversely proportional to the temperatures of electrons that are scattered by ions [6,18].
Let us first examine the parallel component of the thermal force density. Suppose that 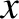 measures
distance along a magnetic field-line. We can write [6,18]
measures
distance along a magnetic field-line. We can write [6,18]
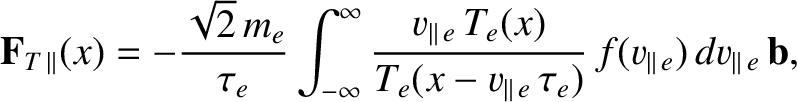 |
(2.308) |
where
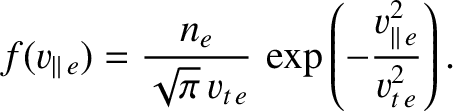 |
(2.309) |
Here, we are making use of the fact that
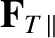 is sum of
is sum of
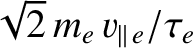 (the
(the
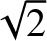 factor is to get agreement with the collisional result), taken over all electrons moving parallel to the field-line, and weighted by the inverse of the electron temperature at the last scattering position. Thus, electrons with parallel velocity
factor is to get agreement with the collisional result), taken over all electrons moving parallel to the field-line, and weighted by the inverse of the electron temperature at the last scattering position. Thus, electrons with parallel velocity
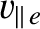 that are scattered by ions at position
that are scattered by ions at position 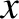 were last scattered
at position
were last scattered
at position
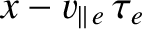 , and are, therefore, characterized by the electron temperature at the latter position.
Suppose that a tearing mode gives rise to a perturbation to the electron temperature along the field-line of the
form
, and are, therefore, characterized by the electron temperature at the latter position.
Suppose that a tearing mode gives rise to a perturbation to the electron temperature along the field-line of the
form
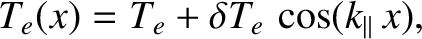 |
(2.310) |
where
 . It follows that
. It follows that
 |
(2.311) |
which reduces to
![$\displaystyle {\bf F}_{T\,\parallel}(x) = -\frac{1}{\sqrt{2}}\,n_e\,\exp\left[-\frac{(k_\parallel\,l_e)^2}{4}\right]\nabla_\parallel T_e.$](img1244.png) |
(2.312) |
Here, use has been made of the result
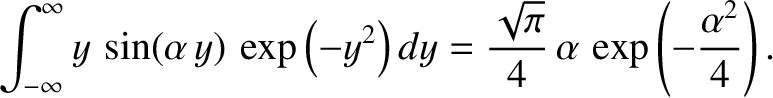 |
(2.313) |
It can be seen that, in the short mean-free-path limit,
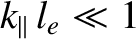 , Equation (2.312) is identical
to Equation (2.306). However, in the long mean-free-path limit,
, Equation (2.312) is identical
to Equation (2.306). However, in the long mean-free-path limit,
 , the parallel thermal
force density is attenuated by a factor
, the parallel thermal
force density is attenuated by a factor
![$\exp[-(k_\parallel\,l_e)^2/4]$](img1248.png) . As is clear from Table 2.1, unless the parallel wavelength of the tearing mode exceeds a few kilometers (i.e., the electron mean-free-path), this attenuation is very strong in a tokamak fusion reactor. Now, tearing modes
are global instabilities of tokamak plasmas, so they have wavelengths that do not differ greatly from the dimensions of the plasma, which is a few meters. Thus, we conclude that there is no parallel component of the thermal force density in a tokamak fusion reactor. To be slightly more exact,
. As is clear from Table 2.1, unless the parallel wavelength of the tearing mode exceeds a few kilometers (i.e., the electron mean-free-path), this attenuation is very strong in a tokamak fusion reactor. Now, tearing modes
are global instabilities of tokamak plasmas, so they have wavelengths that do not differ greatly from the dimensions of the plasma, which is a few meters. Thus, we conclude that there is no parallel component of the thermal force density in a tokamak fusion reactor. To be slightly more exact,
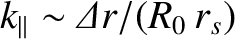 for a tearing mode
in a tokamak plasma, where
for a tearing mode
in a tokamak plasma, where
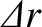 measures radial distance from the rational surface, whose minor radius is
measures radial distance from the rational surface, whose minor radius is 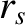 , at which it resonates with the equilibrium magnetic field. (See Section 1.11.) Thus, the attenuation
of the parallel thermal force is strong unless
, at which it resonates with the equilibrium magnetic field. (See Section 1.11.) Thus, the attenuation
of the parallel thermal force is strong unless
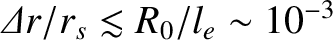 .
.
Let us now consider the perpendicular component of the thermal force density. The appropriate calculation is
analogous to that we just performed, except that electrons that move perpendicular to magnetic field-lines, and are
scattered by ions at a given point in the plasma, can only have originated
from points that are, at most, a few electron gyro-radii away from the given point. Hence, the appropriate attenuation factor is
![$\exp[-(k_\perp\,\rho_e)^2/4]$](img1252.png) . As is clear from Table 2.1, unless the perpendicular wavelength of the tearing mode falls below about 0.1 mm (i.e., the electron gyro-radius), there is no attenuation of the perpendicular thermal force density in a tokamak fusion reactor. Thus, we conclude that Equation (2.307) remains valid in such a reactor.
. As is clear from Table 2.1, unless the perpendicular wavelength of the tearing mode falls below about 0.1 mm (i.e., the electron gyro-radius), there is no attenuation of the perpendicular thermal force density in a tokamak fusion reactor. Thus, we conclude that Equation (2.307) remains valid in such a reactor.
There is also a thermal component of the electron heat flux, which is specified in Equation (2.47). Similar arguments
to those that we just made reveal that the parallel component of this heat flux is strongly attenuated in a tokamak
fusion reactor, due to long mean-free-path effects, whereas the perpendicular component is unaffected.
Consider the diffusive parallel heat flux associated with the electron temperature perturbation (2.310).
In the short mean-free-path limit, we have
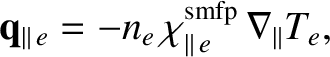 |
(2.314) |
where
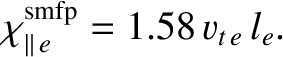 |
(2.315) |
[See Equations (2.44) and (2.48).] On the other hand, in the long mean-free-path (i.e., collisionless) limit [26,27]
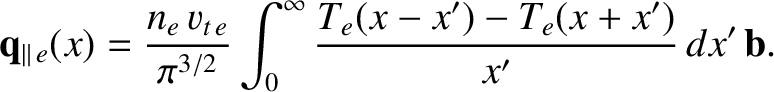 |
(2.316) |
It follows from Equation (2.310) that
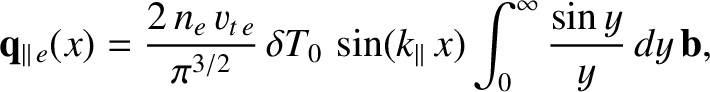 |
(2.317) |
which yields
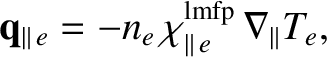 |
(2.318) |
where the long mean-free-path thermal conductivity takes the form [17]
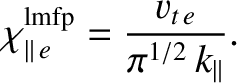 |
(2.319) |
Here, use has been made of the result
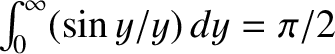 .
It can be seen, from a comparison between Equations (2.315) and (2.319), that the short mean-free-path
parallel electron thermal diffusivity exceeds the collisionless diffusivity when
.
It can be seen, from a comparison between Equations (2.315) and (2.319), that the short mean-free-path
parallel electron thermal diffusivity exceeds the collisionless diffusivity when
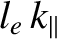 exceeds about unity. However, this is impossible, because the collisionless diffusivity corresponds to the free flow of electrons along
magnetic field-lines, completely unimpeded by collisions, and therefore sets an upper limit on the diffusivity. (Of course, in this limit, the parallel heat flow is not diffusive at all; instead, it is convective.)
Hence,
we conclude that in a tokamak fusion reactor, which is characterized by
exceeds about unity. However, this is impossible, because the collisionless diffusivity corresponds to the free flow of electrons along
magnetic field-lines, completely unimpeded by collisions, and therefore sets an upper limit on the diffusivity. (Of course, in this limit, the parallel heat flow is not diffusive at all; instead, it is convective.)
Hence,
we conclude that in a tokamak fusion reactor, which is characterized by
 , the appropriate expression for the parallel electron thermal “diffusivity” is given by Equation (2.319). Analogous arguments
reveal that the ion parallel thermal “diffusivity” in a tokamak fusion reactor takes the form [17]
, the appropriate expression for the parallel electron thermal “diffusivity” is given by Equation (2.319). Analogous arguments
reveal that the ion parallel thermal “diffusivity” in a tokamak fusion reactor takes the form [17]
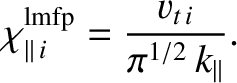 |
(2.320) |
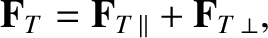
 measures
distance along a magnetic field-line. We can write [6,18]
measures
distance along a magnetic field-line. We can write [6,18]
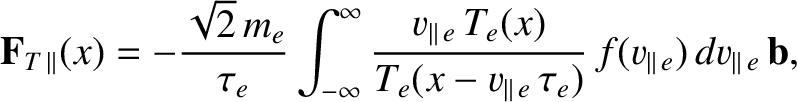
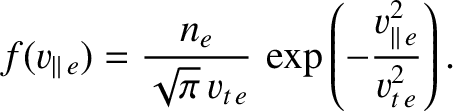
 is sum of
is sum of
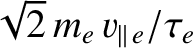 (the
(the
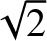 factor is to get agreement with the collisional result), taken over all electrons moving parallel to the field-line, and weighted by the inverse of the electron temperature at the last scattering position. Thus, electrons with parallel velocity
factor is to get agreement with the collisional result), taken over all electrons moving parallel to the field-line, and weighted by the inverse of the electron temperature at the last scattering position. Thus, electrons with parallel velocity
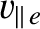 that are scattered by ions at position
that are scattered by ions at position 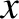 were last scattered
at position
were last scattered
at position
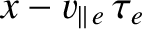 , and are, therefore, characterized by the electron temperature at the latter position.
Suppose that a tearing mode gives rise to a perturbation to the electron temperature along the field-line of the
form
where
, and are, therefore, characterized by the electron temperature at the latter position.
Suppose that a tearing mode gives rise to a perturbation to the electron temperature along the field-line of the
form
where
 . It follows that
. It follows that

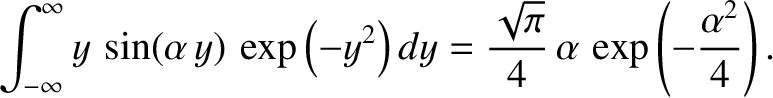
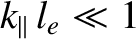 , Equation (2.312) is identical
to Equation (2.306). However, in the long mean-free-path limit,
, Equation (2.312) is identical
to Equation (2.306). However, in the long mean-free-path limit,
 , the parallel thermal
force density is attenuated by a factor
, the parallel thermal
force density is attenuated by a factor
![$\exp[-(k_\parallel\,l_e)^2/4]$](img1248.png) . As is clear from Table 2.1, unless the parallel wavelength of the tearing mode exceeds a few kilometers (i.e., the electron mean-free-path), this attenuation is very strong in a tokamak fusion reactor. Now, tearing modes
are global instabilities of tokamak plasmas, so they have wavelengths that do not differ greatly from the dimensions of the plasma, which is a few meters. Thus, we conclude that there is no parallel component of the thermal force density in a tokamak fusion reactor. To be slightly more exact,
. As is clear from Table 2.1, unless the parallel wavelength of the tearing mode exceeds a few kilometers (i.e., the electron mean-free-path), this attenuation is very strong in a tokamak fusion reactor. Now, tearing modes
are global instabilities of tokamak plasmas, so they have wavelengths that do not differ greatly from the dimensions of the plasma, which is a few meters. Thus, we conclude that there is no parallel component of the thermal force density in a tokamak fusion reactor. To be slightly more exact,
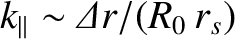 for a tearing mode
in a tokamak plasma, where
for a tearing mode
in a tokamak plasma, where
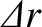 measures radial distance from the rational surface, whose minor radius is
measures radial distance from the rational surface, whose minor radius is 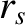 , at which it resonates with the equilibrium magnetic field. (See Section 1.11.) Thus, the attenuation
of the parallel thermal force is strong unless
, at which it resonates with the equilibrium magnetic field. (See Section 1.11.) Thus, the attenuation
of the parallel thermal force is strong unless
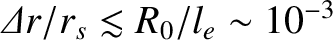 .
.
![$\exp[-(k_\perp\,\rho_e)^2/4]$](img1252.png) . As is clear from Table 2.1, unless the perpendicular wavelength of the tearing mode falls below about 0.1 mm (i.e., the electron gyro-radius), there is no attenuation of the perpendicular thermal force density in a tokamak fusion reactor. Thus, we conclude that Equation (2.307) remains valid in such a reactor.
. As is clear from Table 2.1, unless the perpendicular wavelength of the tearing mode falls below about 0.1 mm (i.e., the electron gyro-radius), there is no attenuation of the perpendicular thermal force density in a tokamak fusion reactor. Thus, we conclude that Equation (2.307) remains valid in such a reactor.
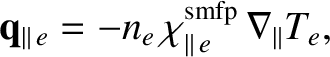
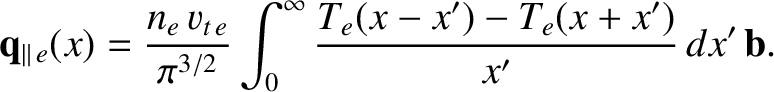
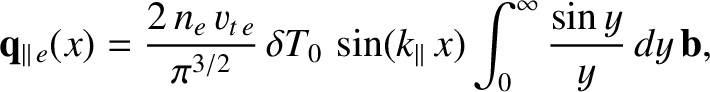
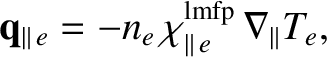
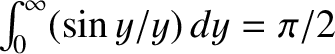 .
It can be seen, from a comparison between Equations (2.315) and (2.319), that the short mean-free-path
parallel electron thermal diffusivity exceeds the collisionless diffusivity when
.
It can be seen, from a comparison between Equations (2.315) and (2.319), that the short mean-free-path
parallel electron thermal diffusivity exceeds the collisionless diffusivity when
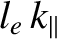 exceeds about unity. However, this is impossible, because the collisionless diffusivity corresponds to the free flow of electrons along
magnetic field-lines, completely unimpeded by collisions, and therefore sets an upper limit on the diffusivity. (Of course, in this limit, the parallel heat flow is not diffusive at all; instead, it is convective.)
Hence,
we conclude that in a tokamak fusion reactor, which is characterized by
exceeds about unity. However, this is impossible, because the collisionless diffusivity corresponds to the free flow of electrons along
magnetic field-lines, completely unimpeded by collisions, and therefore sets an upper limit on the diffusivity. (Of course, in this limit, the parallel heat flow is not diffusive at all; instead, it is convective.)
Hence,
we conclude that in a tokamak fusion reactor, which is characterized by
 , the appropriate expression for the parallel electron thermal “diffusivity” is given by Equation (2.319). Analogous arguments
reveal that the ion parallel thermal “diffusivity” in a tokamak fusion reactor takes the form [17]
, the appropriate expression for the parallel electron thermal “diffusivity” is given by Equation (2.319). Analogous arguments
reveal that the ion parallel thermal “diffusivity” in a tokamak fusion reactor takes the form [17]