Next: Parallel Closure Scheme Up: Plasma Fluid Theory Previous: Neoclassical Transport Contents
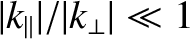 ,
where
,
where
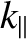 and
and 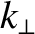 are the wavenumbers of the underlying micro-instabilities parallel and
perpendicular to the equilibrium magnetic field, respectively. An immediate consequence of the flute ordering is
that turbulent eddies generate comparatively little transport parallel to magnetic field-lines. Consequently, we shall
assume that turbulence does not upset the parallel force and heat flux balance described in Equations (2.175)
and (2.176). This implies that the expressions for the in-flux-surface neoclassical ion and electron flows given
in Sections 2.18 and 2.19, well as the expression for the parallel current density given in
Section 2.20, remain valid in the presence of turbulence. We also expect the expressions for the
cross heat fluxes and the gyro-viscous tensors given in Section 2.6 to remain valid, because these effects
are merely a consequence of the rapid gyration of charged particles perpendicular to magnetic field-lines, which is not significantly affected
by turbulence.
On the other hand, we shall replace
our previous expressions for the perpendicular viscous force densities and the perpendicular heat fluxes by phenomenological
terms of the forms
are the wavenumbers of the underlying micro-instabilities parallel and
perpendicular to the equilibrium magnetic field, respectively. An immediate consequence of the flute ordering is
that turbulent eddies generate comparatively little transport parallel to magnetic field-lines. Consequently, we shall
assume that turbulence does not upset the parallel force and heat flux balance described in Equations (2.175)
and (2.176). This implies that the expressions for the in-flux-surface neoclassical ion and electron flows given
in Sections 2.18 and 2.19, well as the expression for the parallel current density given in
Section 2.20, remain valid in the presence of turbulence. We also expect the expressions for the
cross heat fluxes and the gyro-viscous tensors given in Section 2.6 to remain valid, because these effects
are merely a consequence of the rapid gyration of charged particles perpendicular to magnetic field-lines, which is not significantly affected
by turbulence.
On the other hand, we shall replace
our previous expressions for the perpendicular viscous force densities and the perpendicular heat fluxes by phenomenological
terms of the forms
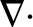 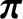 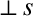 |
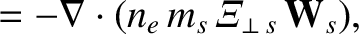 |
(2.303) |
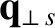 |
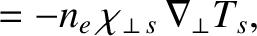 |
(2.304) |
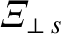 and
and
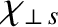 are taken from experimental measurements.
are taken from experimental measurements.
Finally, if axisymmetric tokamak plasmas are to retain their freedom to rotate in the toroidal direction then anomalous transport needs to be intrinsically ambipolar. Fortunately, good theoretical arguments can be made that this is the case [8,29,49].