Next: Resonant Layer Thickness Up: Linear Tearing Mode Stability Previous: Determination of Linear Growth-Rates Contents
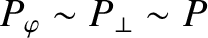 , and
, and
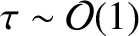 , for
the sake of simplicity.
, for
the sake of simplicity.
Suppose that
 and
and
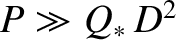 . It follows that
. It follows that  ,
, 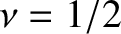 , and
, and
 |
(6.11) |
 |
(6.12) |
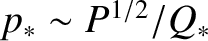 . This so-called resistive-inertial growth-rate regime is valid when
. This so-called resistive-inertial growth-rate regime is valid when
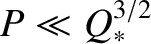 and
and
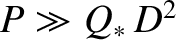 .
Making use of Equations (5.48), (5.54), (5.65), (6.2), and (6.4), the corresponding tearing mode growth-rate is [3]
Here,
.
Making use of Equations (5.48), (5.54), (5.65), (6.2), and (6.4), the corresponding tearing mode growth-rate is [3]
Here,
 is the total diamagnetic frequency [see Equation (5.47)],
is the total diamagnetic frequency [see Equation (5.47)],  is the resistive diffusion timescale [see Equation (5.49)],
and
is the resistive diffusion timescale [see Equation (5.49)],
and
 the energy confinement timescale [see Equation (5.52)]. Note that
the energy confinement timescale [see Equation (5.52)]. Note that 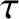 and
and
 are
both assumed to be positive quantities (which is always the case if the electron and ion equilibrium pressure profiles are
monotonically decreasing functions of minor radius). According to the previous equation, the tearing mode is purely oscillatory in the resistive-inertial growth-rate regime.
are
both assumed to be positive quantities (which is always the case if the electron and ion equilibrium pressure profiles are
monotonically decreasing functions of minor radius). According to the previous equation, the tearing mode is purely oscillatory in the resistive-inertial growth-rate regime.
Suppose that
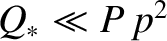 and
and
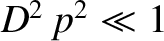 .
It follows that
.
It follows that 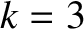 ,
,  , and
, and
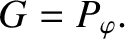 |
(6.14) |
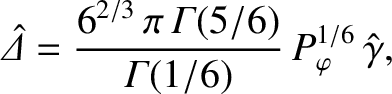 |
(6.15) |
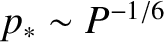 . This so-called viscous-resistive growth-rate regime is valid when
. This so-called viscous-resistive growth-rate regime is valid when
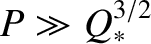 and
and
 .
Making use of Equation (5.53), the corresponding tearing mode growth-rate is [3]
where
.
Making use of Equation (5.53), the corresponding tearing mode growth-rate is [3]
where
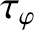 is the momentum confinement timescale [see Equation (5.50)]. We conclude that, in the viscous-resistive growth-rate regime, the tearing mode is a purely growing mode (in a frame of reference that is co-moving with the
electron fluid at the rational surface) when the tearing stability index,
is the momentum confinement timescale [see Equation (5.50)]. We conclude that, in the viscous-resistive growth-rate regime, the tearing mode is a purely growing mode (in a frame of reference that is co-moving with the
electron fluid at the rational surface) when the tearing stability index, 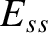 , is positive, and a purely decaying mode
otherwise [4].
, is positive, and a purely decaying mode
otherwise [4].
Suppose that
 and
and
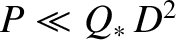 . It follows that
. It follows that  ,
, 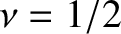 , and
, and
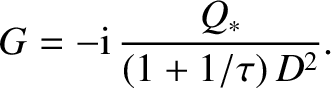 |
(6.17) |
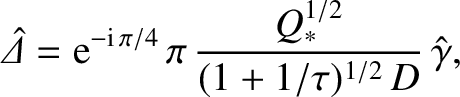 |
(6.18) |
 . This so-called semi-collisional growth-rate regime is valid when
. This so-called semi-collisional growth-rate regime is valid when
 and
and
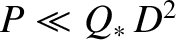 .
Making use of Equation (5.66), the corresponding tearing mode growth-rate is [3]
where
.
Making use of Equation (5.66), the corresponding tearing mode growth-rate is [3]
where 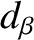 is the ion sound radius [see Equation (4.75)], and
is the ion sound radius [see Equation (4.75)], and 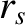 the minor radius of the rational surface. We conclude that,
in the semi-collisional growth-rate regime, the tearing mode is a growing oscillatory mode (in the electron fluid reference frame) when the tearing stability index is positive, and a decaying oscillatory mode
otherwise.
the minor radius of the rational surface. We conclude that,
in the semi-collisional growth-rate regime, the tearing mode is a growing oscillatory mode (in the electron fluid reference frame) when the tearing stability index is positive, and a decaying oscillatory mode
otherwise.
Suppose, finally, that
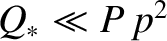 and
and
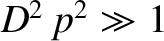 . It follows that
. It follows that 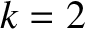 ,
,  , and
, and
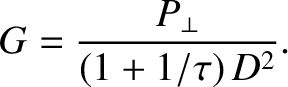 |
(6.20) |
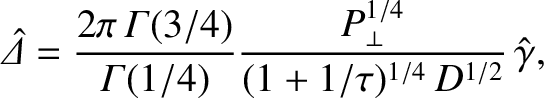 |
(6.21) |
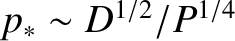 . This so-called diffusive-resistive growth-rate regime is valid when
. This so-called diffusive-resistive growth-rate regime is valid when
 and
and
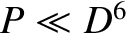 . The corresponding tearing mode growth-rate is [3]
We conclude that, in the diffusive-resistive growth-rate regime, the tearing mode is a purely growing mode (in the electron fluid reference frame) when the tearing stability index is positive, and a purely decaying mode
otherwise.
. The corresponding tearing mode growth-rate is [3]
We conclude that, in the diffusive-resistive growth-rate regime, the tearing mode is a purely growing mode (in the electron fluid reference frame) when the tearing stability index is positive, and a purely decaying mode
otherwise.
Table 5.1 gives estimates for all of the normalized quantities that appear in the layer equation, (6.5), for a low-field and a high-field
fusion reactor. (See Chapter 1.)
Likewise, Table 6.1 gives estimates for all of the unnormalized quantities that appear in the growth-rate formulae (6.13), (6.16),
(6.19), and (6.22) [except for 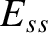 , which is
, which is
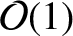 ] for a low-field and a high-field
fusion reactor. (See Chapter 1.)
] for a low-field and a high-field
fusion reactor. (See Chapter 1.)
According to Equations (6.1), (6.3), (6.13), (6.16), (6.19), and (6.22), a linear tearing mode is unstable (except in the resistive-inertial growth-rate regime, in which it is marginally stable) when the tearing stability index, 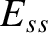 , is positive, and is stable otherwise [4].
Moreover, the perturbed magnetic field associated with the mode co-rotates with the electron fluid at the resonant surface [1]. Finally,
the mode grows on a hybrid timescale that is much greater than the hydrodmagnetic time,
, is positive, and is stable otherwise [4].
Moreover, the perturbed magnetic field associated with the mode co-rotates with the electron fluid at the resonant surface [1]. Finally,
the mode grows on a hybrid timescale that is much greater than the hydrodmagnetic time, 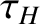 ,
but much less than the resistive evolution time,
,
but much less than the resistive evolution time,  . Note that, in all cases, the growth-rate goes to zero as
. Note that, in all cases, the growth-rate goes to zero as
 . This is not surprising because, as is clear from Equation (5.39), the perturbed
helical magnetic flux at the resonant surface,
. This is not surprising because, as is clear from Equation (5.39), the perturbed
helical magnetic flux at the resonant surface,
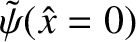 , is constrained to take the value zero
in the limit that
, is constrained to take the value zero
in the limit that
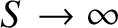 . In other words, magnetic reconnection at the resonant surface (which corresponds to a finite
. In other words, magnetic reconnection at the resonant surface (which corresponds to a finite
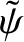 at
at 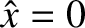 ) is impossible in the absence of plasma resistivity [4].
) is impossible in the absence of plasma resistivity [4].
![\includegraphics[width=1.\textwidth]{Chapter06/Figure6_1.eps}](img2421.png)
|
There are three main factors, other than plasma inertia and resistivity, that
affect the growth-rate of a tearing mode in a conventional tokamak plasma. First, the strength of diamagnetic flows in the plasma, which is parameterized by the
diamagnetic frequency,
 (and by the normalized diamagnetic frequency,
(and by the normalized diamagnetic frequency,  ). Second, the anomalous perpendicular diffusion of momentum and particles, which is parameterized by the momentum and particle confinement
timescales,
). Second, the anomalous perpendicular diffusion of momentum and particles, which is parameterized by the momentum and particle confinement
timescales,
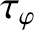 and
and
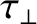 (and by the magnetic Prandtl numbers,
(and by the magnetic Prandtl numbers, 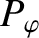 and
and  ). Third, finite ion sound radius effects, which are parameterized by the ion sound radius,
). Third, finite ion sound radius effects, which are parameterized by the ion sound radius, 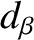 (and by the normalized ion
sound radius
(and by the normalized ion
sound radius  ).
).
There are four tearing-mode growth-rate regimes—the resistive-inertial, the viscous-resistive, the semi-collisional, and the diffusive-resistive—and their extents in  -
-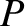 space are illustrated in Figure 6.1 [3].
Note that Figure 6.1 differs somewhat from Figures 5.1 and 5.2 because in the latter two
figures it is assumed that
space are illustrated in Figure 6.1 [3].
Note that Figure 6.1 differs somewhat from Figures 5.1 and 5.2 because in the latter two
figures it is assumed that
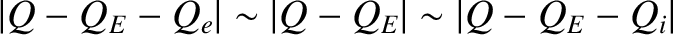 whereas
in the former figure it is assumed that
whereas
in the former figure it is assumed that
 .
This refined ordering eliminates the nonconstant-
.
This refined ordering eliminates the nonconstant- response regimes, and significantly modifies the
extent of the resistive-inertial growth-rate regime. It is clear from Figure 6.1 that a low-field tokamak
fusion reactor lies in the diffusive-resistive growth-rate regime, whereas a high-field tokamak
fusion reactor lies in the viscous-resistive growth-rate regime. (See Section 5.13.)
response regimes, and significantly modifies the
extent of the resistive-inertial growth-rate regime. It is clear from Figure 6.1 that a low-field tokamak
fusion reactor lies in the diffusive-resistive growth-rate regime, whereas a high-field tokamak
fusion reactor lies in the viscous-resistive growth-rate regime. (See Section 5.13.)
The absence of nonconstant- response regimes in Figure 6.1
should come as no surprise. As we saw in Section 5.12, nonconstant-
response regimes in Figure 6.1
should come as no surprise. As we saw in Section 5.12, nonconstant- resonant layers
are characterized by
resonant layers
are characterized by
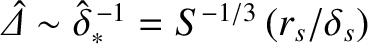 , where
, where  is the radial layer thickness. Hence, according to Equation (6.2), asymptotic matching of such a
layer to the outer solution is only possible if
is the radial layer thickness. Hence, according to Equation (6.2), asymptotic matching of such a
layer to the outer solution is only possible if
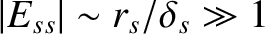 (given that resonant
layers in tokamak plasmas are invariably very thin compared to the minor radius of the plasma). However,
low-
(given that resonant
layers in tokamak plasmas are invariably very thin compared to the minor radius of the plasma). However,
low- tearing modes in conventional tokamak plasmas are characterized by
tearing modes in conventional tokamak plasmas are characterized by
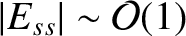 rather than
rather than
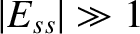 [6]. (As before, we are neglecting
[6]. (As before, we are neglecting 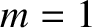 modes, which are characterized by
modes, which are characterized by
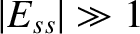 , because they are not really tearing modes.)
, because they are not really tearing modes.)