Next: Determination of Linear Growth-Rates Up: Linear Tearing Mode Stability Previous: Introduction Contents
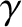 is the growth-rate of the tearing mode, whereas
is the growth-rate of the tearing mode, whereas 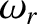 is the real
frequency of the mode in the laboratory frame. We shall assume that
is the real
frequency of the mode in the laboratory frame. We shall assume that
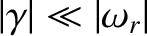 . This assumption can
easily be verified a posteriori. (See Table 6.2.) Asymptotic matching (see Section 3.8) between the tearing mode solution in the outer region and that in the
thin resistive layer, surrounding the rational surface (see Section 3.7), that constitutes the inner region, yields a linear tearing mode dispersion relation of the form
where use has been made of Equations (3.74) and (5.70). Here,
. This assumption can
easily be verified a posteriori. (See Table 6.2.) Asymptotic matching (see Section 3.8) between the tearing mode solution in the outer region and that in the
thin resistive layer, surrounding the rational surface (see Section 3.7), that constitutes the inner region, yields a linear tearing mode dispersion relation of the form
where use has been made of Equations (3.74) and (5.70). Here, 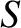 is the Lundquist number at the rational surface [see Equation (5.48)],
is the Lundquist number at the rational surface [see Equation (5.48)], 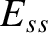 is the real tearing stability index (see Section 3.8),
whereas the complex layer matching parameter,
is the real tearing stability index (see Section 3.8),
whereas the complex layer matching parameter,
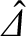 , is defined in Equation (5.69).
, is defined in Equation (5.69).
In a conventional tokamak fusion reactor [assuming that
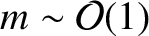 , where
, where  is the poloidal mode number of the tearing perturbation],
is the poloidal mode number of the tearing perturbation],
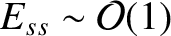 ,6.1 and
,6.1 and
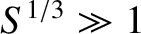 . (See Table 1.5.) Hence, the previous dispersion relation can only be satisfied if
. (See Table 1.5.) Hence, the previous dispersion relation can only be satisfied if 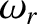 takes a
value that renders
takes a
value that renders
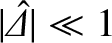 . It is clear from Equations (5.61)–(5.65), (5.93), (5.94), (5.96), and (5.98) that this goal
can be achieved in all of the constant-
. It is clear from Equations (5.61)–(5.65), (5.93), (5.94), (5.96), and (5.98) that this goal
can be achieved in all of the constant- linear response regimes if
linear response regimes if
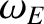 and
and
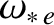 are the E-cross-B and electron diamagnetic frequencies, respectively, at the
rational surface.
[See Equations (5.21), (5.29), (5.44), and (5.45).]
The previous equation implies that the tearing mode co-rotates with the electron fluid at the rational surface [1]. (See Section 2.24.)
are the E-cross-B and electron diamagnetic frequencies, respectively, at the
rational surface.
[See Equations (5.21), (5.29), (5.44), and (5.45).]
The previous equation implies that the tearing mode co-rotates with the electron fluid at the rational surface [1]. (See Section 2.24.)