Next: Response Regimes in Tokamak Up: Linear Resonant Response Model Previous: Nonconstant- Linear Resonant Response Contents
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
![\includegraphics[width=1.\textwidth]{Chapter05/Figure5_1.eps}](img2268.png)
|
Table 5.2 summarizes the properties of the various linear resonant response regimes found in Sections 5.9 and 5.11. Here, we have made use of the abbreviations
In addition, Figures 5.1 and 5.2 show the extents of the various different response regimes in -
-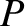 space for the
cases
space for the
cases 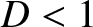 and
and 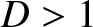 , respectively.
, respectively.
![\includegraphics[width=1.\textwidth]{Chapter05/Figure5_2.eps}](img2279.png)
|
Let
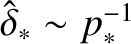 be the normalized radial thickness of the resonant layer. Of course, the true thickness is
be the normalized radial thickness of the resonant layer. Of course, the true thickness is
 . It follows from
Equation (5.69) that the relative change in the perturbed helical magnetic flux,
. It follows from
Equation (5.69) that the relative change in the perturbed helical magnetic flux,
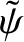 , across the layer
is
, across the layer
is
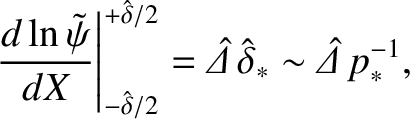 |
(5.114) |
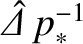 takes the respective values
takes the respective values 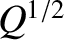 ,
,
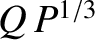 ,
,
 , and
, and
 in the resistive-inertial, viscous-resistive, semi-collisional, and
diffusive-resistive response regimes. Moreover, it is clear from Figures 5.1 and 5.2 that these values are all
much less than unity. In other words, it is indeed the case that
in the resistive-inertial, viscous-resistive, semi-collisional, and
diffusive-resistive response regimes. Moreover, it is clear from Figures 5.1 and 5.2 that these values are all
much less than unity. In other words, it is indeed the case that
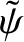 does not vary substantially across a
“constant-
does not vary substantially across a
“constant- ” resonant layer. On the other hand, according to the analysis of Section 5.11,
” resonant layer. On the other hand, according to the analysis of Section 5.11,
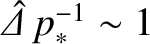 in the inertial,
viscous-inertial, and diffusive-inertial response regimes, which implies that
in the inertial,
viscous-inertial, and diffusive-inertial response regimes, which implies that
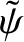 does vary substantially
across a “nonconstant-
does vary substantially
across a “nonconstant- ” layer.
” layer.