According to Equation (6.25), the time evolution of the reconnected magnetic
flux (in a frame of reference that co-rotates with the magnetic island chain) in the linear regime is
governed by
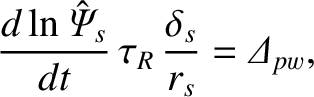 |
(9.6) |
where  is the linear layer width. The previous equation can be rearranged to give
is the linear layer width. The previous equation can be rearranged to give
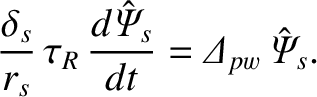 |
(9.7) |
Now, given that
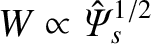 [see Equation (8.1)], the Rutherford island width
evolution equation, (9.5), can be rewritten in the form
[see Equation (8.1)], the Rutherford island width
evolution equation, (9.5), can be rewritten in the form
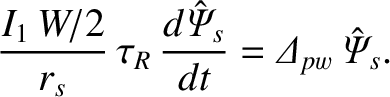 |
(9.8) |
It can be seen, via a comparison between the previous two equations, that a nonlinear magnetic island
chain evolves in time in an analogous fashion to a linear layer whose width is 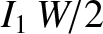 . In other words, the
essential nonlinearity in the nonlinear regime comes about because the effective layer width is amplitude
dependent.
. In other words, the
essential nonlinearity in the nonlinear regime comes about because the effective layer width is amplitude
dependent.
Now, Equation (9.7) is valid when
 (i.e., when the linear layer width is much greater than the island
width), whereas Equation (9.8) is valid in the opposite limit. This observation allows us to formulate a composite time evolution equation that encompasses both the linear and the nonlinear regimes [3,4,8,10]:
(i.e., when the linear layer width is much greater than the island
width), whereas Equation (9.8) is valid in the opposite limit. This observation allows us to formulate a composite time evolution equation that encompasses both the linear and the nonlinear regimes [3,4,8,10]:
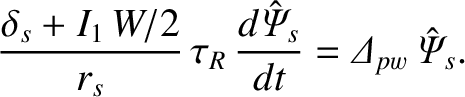 |
(9.9) |
The previous equation can also be written
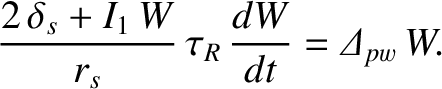 |
(9.10) |
Figure 9.1:
Time evolution of the magnetic island width predicted by the composite linear/nonlinear model.
|
|
Let
Equation (9.10) transforms into
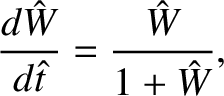 |
(9.13) |
which can be solved to give
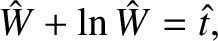 |
(9.14) |
assuming that 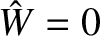 at
at
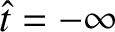 .
Figure 9.1 shows the time evolution of the magnetic island width predicted by the previous equation. It
can be seen that the evolution makes a smooth transition from exponential growth when
.
Figure 9.1 shows the time evolution of the magnetic island width predicted by the previous equation. It
can be seen that the evolution makes a smooth transition from exponential growth when
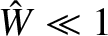 (i.e., when the island width is much less than the linear layer width) to algebraic growth
when
(i.e., when the island width is much less than the linear layer width) to algebraic growth
when
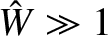 (i.e., when the island width is much greater than the linear layer width).
(i.e., when the island width is much greater than the linear layer width).
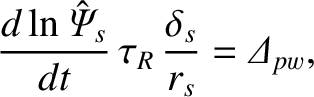
 is the linear layer width. The previous equation can be rearranged to give
Now, given that
is the linear layer width. The previous equation can be rearranged to give
Now, given that
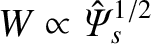 [see Equation (8.1)], the Rutherford island width
evolution equation, (9.5), can be rewritten in the form
It can be seen, via a comparison between the previous two equations, that a nonlinear magnetic island
chain evolves in time in an analogous fashion to a linear layer whose width is
[see Equation (8.1)], the Rutherford island width
evolution equation, (9.5), can be rewritten in the form
It can be seen, via a comparison between the previous two equations, that a nonlinear magnetic island
chain evolves in time in an analogous fashion to a linear layer whose width is 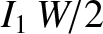 . In other words, the
essential nonlinearity in the nonlinear regime comes about because the effective layer width is amplitude
dependent.
. In other words, the
essential nonlinearity in the nonlinear regime comes about because the effective layer width is amplitude
dependent.
 (i.e., when the linear layer width is much greater than the island
width), whereas Equation (9.8) is valid in the opposite limit. This observation allows us to formulate a composite time evolution equation that encompasses both the linear and the nonlinear regimes [3,4,8,10]:
(i.e., when the linear layer width is much greater than the island
width), whereas Equation (9.8) is valid in the opposite limit. This observation allows us to formulate a composite time evolution equation that encompasses both the linear and the nonlinear regimes [3,4,8,10]:
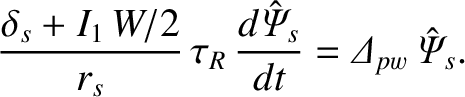
![\includegraphics[width=1.\textwidth]{Chapter09/Figure9_1.eps}](img2959.png)
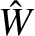
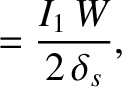
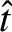
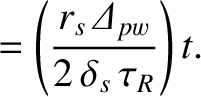
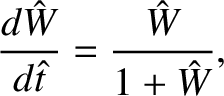
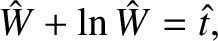
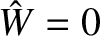 at
at
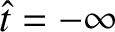 .
Figure 9.1 shows the time evolution of the magnetic island width predicted by the previous equation. It
can be seen that the evolution makes a smooth transition from exponential growth when
.
Figure 9.1 shows the time evolution of the magnetic island width predicted by the previous equation. It
can be seen that the evolution makes a smooth transition from exponential growth when
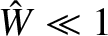 (i.e., when the island width is much less than the linear layer width) to algebraic growth
when
(i.e., when the island width is much less than the linear layer width) to algebraic growth
when
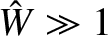 (i.e., when the island width is much greater than the linear layer width).
(i.e., when the island width is much greater than the linear layer width).