Next: Composite Linear/Nonlinear Model Up: Nonlinear Tearing Mode Stability Previous: Introduction Contents
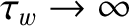 , where
, where 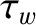 is the time constant of the wall—see Section 3.10), and that there is no current
flowing through the external magnetic field-coil [i.e.,
is the time constant of the wall—see Section 3.10), and that there is no current
flowing through the external magnetic field-coil [i.e.,
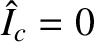 , where
, where 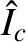 is the normalized coil current—see Equation (3.194)]. In this case, Equations (3.187),
(3.188), and (7.5), yield
where
is the normalized coil current—see Equation (3.194)]. In this case, Equations (3.187),
(3.188), and (7.5), yield
where
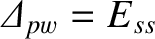 is the (real dimensionless) perfect-wall tearing stability index,
is the (real dimensionless) perfect-wall tearing stability index,
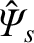 the normalized reconnected helical magnetic flux at the rational surface [see Equation (3.184)],
and
the normalized reconnected helical magnetic flux at the rational surface [see Equation (3.184)],
and
 the normalized helical sheet current density at the rational surface [see Equation (3.183)]. It is clear from the previous equation that
which implies that zero electromagnetic torque is exerted at the rational surface. (See Section 3.13.)
the normalized helical sheet current density at the rational surface [see Equation (3.183)]. It is clear from the previous equation that
which implies that zero electromagnetic torque is exerted at the rational surface. (See Section 3.13.)
Equation (9.2) yields
which can be combined with Equations (8.1), (8.108), and (9.3) to give the so-called Rutherford island width evolution equation [13]: Here,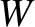 is the full radial width of the magnetic island chain that develops at the rational surface,
is the full radial width of the magnetic island chain that develops at the rational surface, 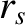 the
minor radius of the surface, and
the
minor radius of the surface, and
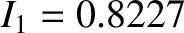 [see Equation (8.124)].
We conclude that, in the nonlinear regime, the width of the magnetic
island chain grows algebraically in time on the resistive diffusion time,
[see Equation (8.124)].
We conclude that, in the nonlinear regime, the width of the magnetic
island chain grows algebraically in time on the resistive diffusion time,  . Obviously, this is a much slower time evolution than that predicted in the linear regime.
. Obviously, this is a much slower time evolution than that predicted in the linear regime.