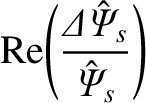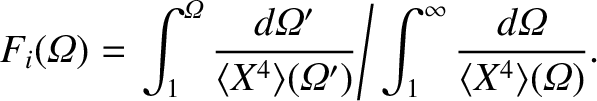Asymptotic Matching
Now that we have found the solution of our rescaled, reduced, drift-MHD equations in the immediate vicinity of the magnetic island chain, it is
necessary to asymptotically match this solution to the solution in the outer region.
Given that
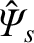 is real, it follows from
Equations (3.72), (3.73), (3.183), (3.184), and (8.9) that
Making use of Equations (8.1) and (8.11), we obtain
However, according to Equations (8.20) and (8.53),
is real, it follows from
Equations (3.72), (3.73), (3.183), (3.184), and (8.9) that
Making use of Equations (8.1) and (8.11), we obtain
However, according to Equations (8.20) and (8.53),
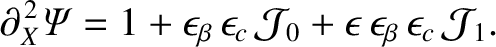 |
(8.95) |
Moreover, it is clear from Equations (8.80) and (8.85) that
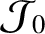 has the symmetry of
has the symmetry of 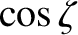 ,
whereas
,
whereas
 has the symmetry of
has the symmetry of 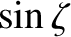 .
Hence, we deduce that
The previous two equations can also be written
Here, we have made use of the fact that
.
Hence, we deduce that
The previous two equations can also be written
Here, we have made use of the fact that
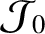 and
and
 are both even functions of
are both even functions of 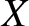 , as well
as the easily proved results
, as well
as the easily proved results
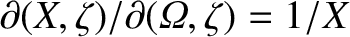 and
and
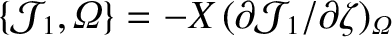 .
.
Equations (8.85) and (8.99) can be combined to give [5]
where use has been made of the facts that 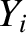 is zero inside the island separatrix,
is zero inside the island separatrix, 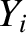 is continuous across the separatrix, and
is continuous across the separatrix, and
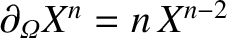 .
Combining the previous equation with Equation (8.87), we obtain [5]
.
Combining the previous equation with Equation (8.87), we obtain [5]
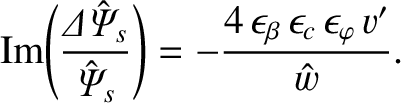 |
(8.101) |
The previous equation yields
![$\displaystyle \left[r\,\frac{d\omega_E}{dr}\right]_{r_{s-}}^{r_{s+}} = \left(\f...
...t){\rm Im}\!\left(\frac{{\mit\Delta}\hat{\mit\Psi}_s}{\hat{\mit\Psi}_s}\right),$](img2891.png) |
(8.102) |
where use has been made of Equations (8.23), (8.25), (8.27), and (8.46), as well as
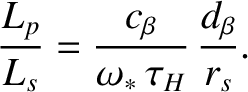 |
(8.103) |
Here, 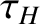 is the hydromagnetic time [see Equation (5.43)]. Equation (8.102) can also be obtained by integrating Equation (3.165) across the rational surface, making use of Equation (3.140), as well as the
identification
is the hydromagnetic time [see Equation (5.43)]. Equation (8.102) can also be obtained by integrating Equation (3.165) across the rational surface, making use of Equation (3.140), as well as the
identification
![$\displaystyle \left[r\,\frac{d\omega_E}{dr}\right]_{r_{s-}}^{r_{s+}} = m\left[r\,\frac{\partial{\mit\Delta\Omega}_\theta}{\partial r}\right]_{r_{s-}}^{r_{s+}}.$](img2893.png) |
(8.104) |
The previous identification merely states that the discontinuity in the MHD fluid velocity gradient that develops in the outer region at the rational
surface is mirrored by an equal discontinuity in the ion fluid velocity gradient (because the discontinuity is ultimately due to
a discontinuity in the E-cross-B velocity gradient, and there is no discontinuity in the diamagnetic velocity gradient).
Equations (8.80) and (8.98) can be combined to give
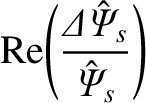 |
 |
(8.105) |
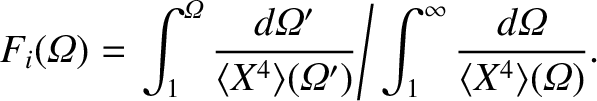 |
(8.107) |
Finally, Equations (8.10), (8.23)–(8.27), (8.101), (8.103), and (8.106)
give [6,12]
where
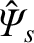 is real, it follows from
Equations (3.72), (3.73), (3.183), (3.184), and (8.9) that
is real, it follows from
Equations (3.72), (3.73), (3.183), (3.184), and (8.9) that
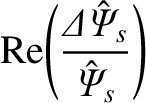
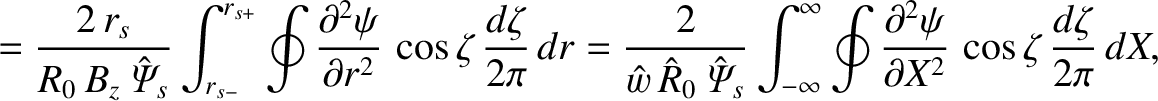
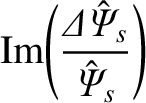
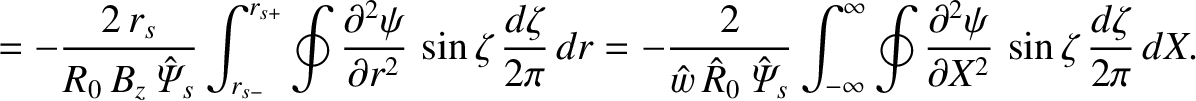
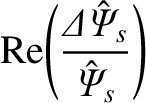
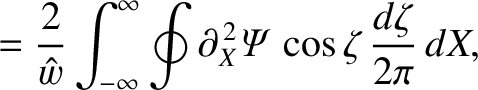
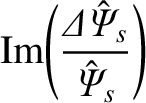
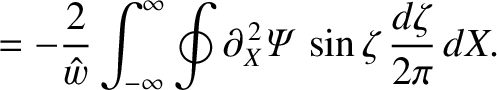
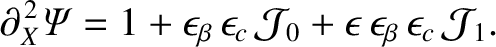
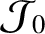 has the symmetry of
has the symmetry of 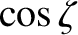 ,
whereas
,
whereas
 has the symmetry of
has the symmetry of 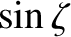 .
Hence, we deduce that
.
Hence, we deduce that
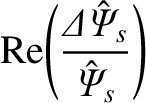
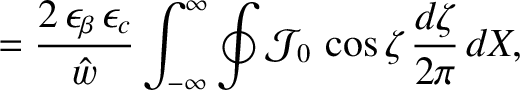
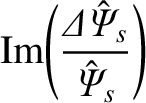
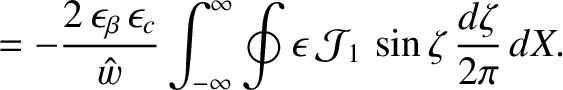
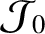 and
and
 are both even functions of
are both even functions of 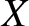 , as well
as the easily proved results
, as well
as the easily proved results
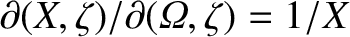 and
and
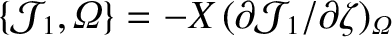 .
.
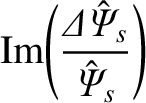
![$\displaystyle =\frac{4\,\epsilon_\beta\,\epsilon_c\,\epsilon_\varphi}{\hat{w}}\...
...ga}(\vert X\vert^3\,\partial_{\mit\Omega}Y_i)\right]\right\rangle d{\mit\Omega}$](img2886.png)
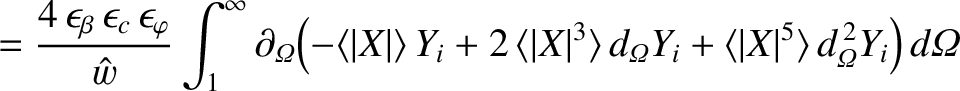
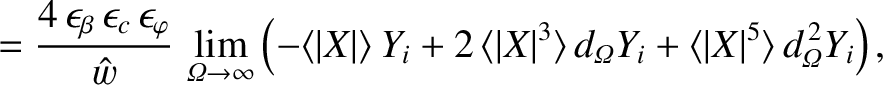
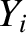 is zero inside the island separatrix,
is zero inside the island separatrix, 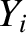 is continuous across the separatrix, and
is continuous across the separatrix, and
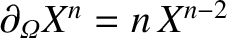 .
Combining the previous equation with Equation (8.87), we obtain [5]
The previous equation yields
where use has been made of Equations (8.23), (8.25), (8.27), and (8.46), as well as
Here,
.
Combining the previous equation with Equation (8.87), we obtain [5]
The previous equation yields
where use has been made of Equations (8.23), (8.25), (8.27), and (8.46), as well as
Here, 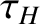 is the hydromagnetic time [see Equation (5.43)]. Equation (8.102) can also be obtained by integrating Equation (3.165) across the rational surface, making use of Equation (3.140), as well as the
identification
is the hydromagnetic time [see Equation (5.43)]. Equation (8.102) can also be obtained by integrating Equation (3.165) across the rational surface, making use of Equation (3.140), as well as the
identification
![$\displaystyle \left[r\,\frac{d\omega_E}{dr}\right]_{r_{s-}}^{r_{s+}} = m\left[r\,\frac{\partial{\mit\Delta\Omega}_\theta}{\partial r}\right]_{r_{s-}}^{r_{s+}}.$](img2893.png)