Next: Lowest-Order Solution Up: Nonlinear Resonant Response Model Previous: Rescaled Reduced Drift-MHD Model Contents
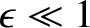 .
.
Table 5.1 gives estimates for the values of the various parameters that characterize the rescaled reduced drift-MHD model, (8.16)–(8.20), in a low-field
and a high-field tokamak fusion reactor. (See Chapter 1.) These estimates are made using the following assumptions:
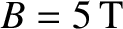 (low-field) or
(low-field) or
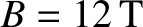 (high-field),
(high-field),
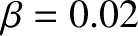 ,
,
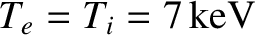 ,
,
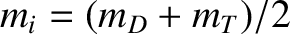 (where
(where 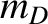 and
and 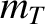 are the deuteron and triton masses, respectively),
are the deuteron and triton masses, respectively),
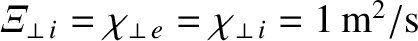 ,
, 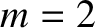 ,
, 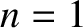 ,
, 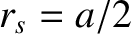 (where
(where 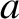 is the minor radius of the plasma),
is the minor radius of the plasma), 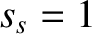 ,
, 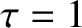 ,
,
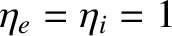 , and
, and
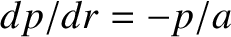 . It is clear from Table 5.1 and Equations (8.25)–(8.34) that all of the
. It is clear from Table 5.1 and Equations (8.25)–(8.34) that all of the 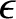 parameters appearing in the
rescaled, reduced, drift-MHD equations are less than unity, in accordance with Equation (8.47), provided that the
radial width of the magnetic island chain that develops in the inner region exceeds a few centimeters.
parameters appearing in the
rescaled, reduced, drift-MHD equations are less than unity, in accordance with Equation (8.47), provided that the
radial width of the magnetic island chain that develops in the inner region exceeds a few centimeters.
The orderings
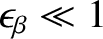 and
and
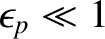 are a direct consequence of the fact that conventional tokamak
fusion reactors have large aspect-ratios (i.e.,
are a direct consequence of the fact that conventional tokamak
fusion reactors have large aspect-ratios (i.e.,
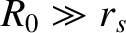 ), and confine low-
), and confine low-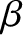 plasmas (i.e.,
plasmas (i.e.,
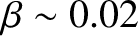 ).
As will become apparent, the ordering
).
As will become apparent, the ordering
 ensures that the island chain is
sufficiently wide that ion acoustic waves propagating parallel to the magnetic field are able to smooth out any
variations in the normalized plasma pressure,
ensures that the island chain is
sufficiently wide that ion acoustic waves propagating parallel to the magnetic field are able to smooth out any
variations in the normalized plasma pressure, 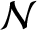 , around magnetic flux-surfaces [9].
The orderings
, around magnetic flux-surfaces [9].
The orderings
 ,
,
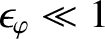 , and
, and
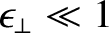 ensure that the island
chain is sufficiently wide that the perpendicular diffusion of magnetic flux, momentum, and energy are not dominant
effects in the rescaled, reduced, drift-MHD equations. Finally, the ordering
ensure that the island
chain is sufficiently wide that the perpendicular diffusion of magnetic flux, momentum, and energy are not dominant
effects in the rescaled, reduced, drift-MHD equations. Finally, the ordering
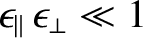 ensures that the island chain is sufficiently wide that parallel energy transport smooths out any variations in the normalized plasma pressure,
ensures that the island chain is sufficiently wide that parallel energy transport smooths out any variations in the normalized plasma pressure, 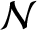 , around magnetic flux-surfaces [3].
, around magnetic flux-surfaces [3].
Finally, suppose that
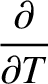 |
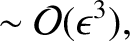 |
(8.48) |
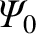 ,
,
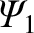 , et cetera are assumed to be
, et cetera are assumed to be
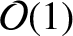 in the inner region.
in the inner region.